When it comes to both protecting and using sensitive data, fully homomorphic encryption is a technology that offers security and peace of mind. By maintaining full cryptographic security for data at every stage, including during processing, FHE enables data scientists and developers to collaboratively apply common data analysis tools to the most valuable information without the risks that we commonly associate with data sharing.
Applying machine learning models under this model of computing introduces some additional hurdles that need to be overcome. However, modern FHE libraries are now making FHE increasingly easy to use without the need for expert knowledge in cryptography.
To demonstrate this, Optalysys offered an undergraduate internship over the summer of 2022. The goal of this internship was to introduce a student to the world of encrypted data science, and see what was possible given the current state of the field.
Our intern for 2022, Peter Li, was a second-year (now third-year) undergraduate studying engineering at Cambridge University. Peter’s work focused on the deployment of common machine learning models in the FHE space, and his article below covers the application of the Zama Concrete library to several different network models and data-sets.
For data scientists looking to make the transition into working safely with highly sensitive information, this article features examples of the implementation and execution of several different machine learning techniques in encrypted space.
More broadly, if you’re an organisation looking for the next significant step in data science, Peter’s work demonstrates that developing useful FHE implementations is now well within scope for data specialists. When paired with Optalysys technology that allows FHE to be deployed at scale and over large data sets, the market for novel applications and services running on previously untouchable data will be primed for massive growth.
That’s all from us at Optalysys for now; we’ll leave you with Peter’s article below. We’ll be back with our own work on FHE and optical computing in the near future.
Machine learning is a domain of AI dealing with systems that can learn patterns from existing data, and then use this learnt information to make predictions about new data. Since 2010, incredibly rapid progress has been made in both the fundamental data science and deployment of machine learning, particularly in the associated domain of deep learning. So what is it that has pushed machine learning to become so prominent?
There are many reasons why, but a good starting point would be our own abilities with respect to data. Humans are conditioned to think and work in three dimensions: this means we can readily visualise and understand the relationships between datasets with three or fewer variables.
Unfortunately, many useful sets of data collected in the real world do not fit that criteria. Datasets with tens or hundreds of variables are commonplace in data science, and although there are techniques for doing so, it would be very difficult for humans to understand all the key relationships between variables. And if you were dealing with, say, a multi-megapixel image for computer vision, you’ll be looking at millions of variables. Needless to say, trying to hand-programme an effective general image recognition algorithm would be a hopeless endeavour.
This is where machine learning comes in. The ability of computers to pick up on relationships that are otherwise locked away in complex multivariate data sets, and then make predictions based on that information, is incredibly useful for countless applications spanning many different industries. These include things features we take for granted in our daily lives, such as personalised recommendations given by the likes of Netflix and Spotify, to things we don’t often think about such as analysing market data for automated high-frequency trading.
We often attribute the popularity of ML to recent advances in deep learning. This is indeed true, although it is important to remember that the reason why ML can be used on such a wide scale is thanks to the more holistic improvements in computing infrastructure, as well as the unprecedented abundance of data.
Back in 2012, IBM said that 90% of all data ever generated by humanity was in the past two years. The rate of data creation has only accelerated since then. Data is essential for training machine learning algorithms, and increasingly powerful models have come into existence as we harvest ever more of it.
More powerful models also require vast quantities of storage and compute power, especially in the case of deep learning. More data also means more infrastructure is needed for storage, processing and (secure) transmission of this data. As a result, there has been an increased use of cloud computing for machine learning applications.
The rise of cloud computing, alongside ever improving computer hardware, addresses the problem of high resource demand for machine learning. It allows companies to outsource the intensive computation associated with ML on a ‘pay for what you need’ basis to third-party servers, which save them the capital cost of buying new hardware. With the growing popularity of machine learning, increasing complexities of deep learning models, and ever increasing quantities of data involved in both training and inference, this trend of machine learning moving to the cloud is unlikely to slow down.
Various large cloud providers now offer Machine Learning as a Service (MLaaS) that help machine learning teams worldwide with tasks such as data preprocessing, model training, tuning and evaluation, or just straight up Inference as a Service (IaaS). Providers include Microsoft Azure, AWS, Google Cloud Platform and IBM Watson.
A movement to the Cloud comes with privacy and security concerns. For many applications of ML, the data which serves as the foundation for training or making predictions may be sensitive information that the owners would like to keep confidential. An example would be predictive diagnostics in healthcare. If the machine learning model is hosted on the Cloud, then this would involve the hospital sending sensitive health data to a third party Cloud provider. Another example would be predictive analysis of credit score, which would involve sending large quantities of sensitive financial data to a third party provider.
The involvement of a third party increases the risk of data leaks considerably. Even though data is encrypted during transmission, it must be decrypted once it reaches the third party provider where the ML model is hosted, in order for it to be used. This creates a sufficient window for the sensitive data to become compromised, whether through exfiltration by malicious insiders or external hacking attacks. In 2019, there had been over 5000 confirmed instances of data breaches, with billions of personal files leaked. When it comes to Cloud providers given access to large quantities of potentially sensitive data, such risks are not negligible.
There are of course techniques for preprocessing data to obfuscate the confidential parts of it, but these cannot be solely relied upon. Too much restriction, and the data loses much of its utility. Too little, and there is a significant risk of de-anonymisation.
Fortunately, there are promising privacy enhancing technologies (PETs) in development that offer the prospect of being able to enjoy the benefits of machine learning in the cloud without introducing the risks that lead to privacy concerns.
The biggest game changer in this category is FHE — Fully Homomorphic Encryption. The concept of homomorphic encryption is straightforward to understand: you can perform whatever calculation you want directly on the encrypted data, without having to decrypt it first.
When you do finally decrypt it (usually when it’s back in safe hands, such as with the original data owner), the output is the same as if you had performed the calculation on the underlying cleartext.
As simple as it sounds, this makes FHE the Holy Grail of cryptography: currently we can securely encrypt data when in transit or storage, but not when data is being processed. Much of the vulnerability of data in the cloud stems from this reason, and FHE addresses this gap.
Once confidential data is sent to the cloud, it would remain encrypted for its entire journey, and any computation can be performed on the ciphertext. After the desired result (still encrypted) is sent back to the owner of the data, they can use the secret key which only they have access to, to decrypt it and obtain the desired result.
The idea of homomorphic encryption has been around for decades, since the first work following the introduction of RSA (which is itself partially homomorphic) in the late seventies.
However, though there had been partially homomorphic encryption and somewhat homomorphic encryption schemes through the years, it wasn’t until 2009 when Craig Gentry published the whitepaper for the first ever Fully Homomorphic Encryption scheme. Since then considerable progress had been made by researchers on newer generations of FHE schemes, but there have been technical challenges that kept FHE largely confined to research papers.
By far the biggest of these barriers is speed; current FHE schemes are impractically slow when executed on conventional computers — up to 1,000,000 times slower than the equivalent operation performed in plaintext. Despite these challenges, significant progress is being made in bringing the advantages of FHE closer to mass adoption than ever.
Another key appeal of current FHE schemes is that they are quantum safe due to their mathematical basis in the Learning with Errors problems, which are secure even against known attacks by quantum computers, which most contemporary encryption techniques are vulnerable against.
Optalysys are developing specialist hardware for tackling the speed issues of FHE, combining the capabilities of optical computing and silicon photonics with electronics designed around FHE workloads. Efficient hardware is itself a holy grail for FHE, as conventional computing is simply never going to be well suited to the kind of calculations it requires.
On the developer side, there are a number of increasingly advanced open source libraries that support FHE computation, including those developed by big players in the tech world: SEAL by Microsoft, and HElib developed by IBM, as well as the Google FHE transpiler. We are also particularly interested in the OpenFHE project, spearheaded by Duality, which aims to unify most of the current FHE schemes and features as well as developing new ones such as scheme-switching. The library we use in this article is the Concrete library, developed by the French company Zama.
The key mission of Concrete is to allow developers to easily convert programs to run with FHE. The specific FHE scheme on which Concrete operates is called TFHE; whenever we talk about the properties of FHE in the context of this article, we are specifically describing the properties of TFHE.
The core TFHE library is written in Rust, but they also have two Python APIs: Concrete Numpy, which converts regular Numpy operations into equivalent FHE circuits; and Concrete ML, an API designed for machine learning developers, that has the capability of converting entire ML models directly into FHE.
In the rest of the article we will focus on the framework Concrete ML, and how it offers a glimpse into a future where data can be passed to machine learning models without ever compromising privacy.
Despite still being in the alpha stage of development, Concrete ML already proved remarkably easy to use. It allows a user to convert entire machine learning models written in the popular ML frameworks of Scikit-learn and PyTorch directly into their FHE equivalent with sometimes only a few extra lines of code.
Machine learning is often split into the categories of supervised, unsupervised and reinforcement learning. It is worth noting that Concrete ML currently (version 0.2, but version 0.3 has since been released) only supports supervised learning, where the model is trained using labelled data.
Here, we put together three simple machine learning models that tackle different problems that reflect real world applications for FHE. All three of the problems fall under the category of classification problems, including both binary and multiclass classification. We will present one example from each of the below categories:
This is a very simple dataset available to be readily imported from the Scikit-Learn library, used for testing ML algorithms on binary classification. While a very simple model on a small dataset, it links closely to an area where we see great potential for FHE deployment: diagnostic analytics.
Machine learning models have become increasingly apt at predicting the likelihood of a patient having particular diseases, especially with the ever increasing wealth of medical data available. However, medical data also tend to be confidential in nature, and there are increasing privacy concerns as patient data becomes more and more digitised.
Below we demonstrate how FHE can be used to encrypt data when passed through a machine learning model for inference. For the sake of brevity, we’ll only focus on certain operations; an associated Jupyter notebook can be found here. We’ll start with our pre-processing of the Scikit-Learn Breast Cancer dataset.
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import datasets
data = datasets.load_breast_cancer()
bc = pd.DataFrame(data.data, columns = data.feature_names)
bc['class'] = data.target
from mlxtend.feature_selection import SequentialFeatureSelector as SFS
from sklearn.pipeline import make_pipeline
from sklearn.model_selection import KFold
from sklearn.linear_model import LogisticRegression
cv = KFold(n_splits=10, random_state=None, shuffle=False)
classifier_pipeline = make_pipeline(LogisticRegression())
sfs1 = SFS(classifier_pipeline,
k_features=20,
forward=True,
scoring='neg_log_loss',
cv=cv
)
sfs1.fit(bc.drop(columns='class'), bc['class'])
sfs1.subsets_
Data pre-processing is perhaps the most important and time-consuming part of building a machine learning workflow. The breast cancer dataset has 30 explanatory variables, many of which give negligible contributions to model accuracy. Therefore, using the forward feature selection tool from the library Mlxtend, we identified lists of the most helpful features, from 1 to 20 in length.
The negative logarithmic loss scores are as follows, worked out using Sklearn’s regular logistic regression function:
Number of features selected, Negative logarithmic loss 1, -0.1883 2, -0.1473 5, -0.1103 10, -0.1044 20, -0.1032
We can see that once we have identified 10 of the best features, adding additional features only give very marginal gains in model accuracy, and hence we proceed with 10 explanatory variables for the FHE model.
In the below, we use these explanatory variables to construct 3 versions of a logistic regression. The first is a “typical” unencrypted example. The second and third are, respectively, a version in which the data is quantised to the same precision as can be achieved using TFHE (but not encrypted), and a version which executes the logistic regression using Concrete ML.
import numpy as np
from sklearn.model_selection import train_test_split
from concrete.ml.sklearn import LogisticRegression as ConcreteLogisticRegression
from sklearn.preprocessing import RobustScaler
# Below are the ten features that contribute the most to model accuracy
selected_features_10 = [
'mean compactness',
'mean concave points',
'radius error',
'area error',
'worst texture',
'worst perimeter',
'worst area',
'worst smoothness',
'worst concave points',
'worst symmetry'
]
logreg = LogisticRegression()
logreg.fit(X_train, y_train)
y_pred_test = np.asarray(logreg.predict(X_test))
sklearn_acc = np.sum(y_pred_test == y_test) / len(y_test) * 100
q_logreg = ConcreteLogisticRegression(n_bits={"inputs": 5, "weights": 2})
q_logreg.fit(X_train, y_train)
q_logreg.compile(X_train)
q_y_pred_test = q_logreg.predict(X_test)
quantized_accuracy = (q_y_pred_test == y_test).mean() * 100
q_y_pred_fhe = q_logreg.predict(X_test, execute_in_fhe=True)
homomorphic_accuracy = (q_y_pred_fhe == y_test).mean() * 100
print(f"Regular Sklearn model accuracy: {sklearn_acc:.4f}%")
print(f"Clear quantised model accuracy: {quantized_accuracy:.4f}%")
print(f"Homomorphic model accuracy: {homomorphic_accuracy:.4f}")
The outcomes are as follows:
First, we will briefly talk about what is meant by ‘Clear quantised model’. One constraint of modern FHE methods, including TFHE — which the Concrete framework is based upon — is that the internal calculations are constrained to operations over specific numerical representations. This includes integers (BGV, BFV) and fixed-point values (CKKS). This may sound like a problem; being able to use efficient number representations to represent the parameters and inputs for a given model is something we take for granted in unencrypted computing.
The examples shown here demonstrate that this is not necessarily the case — we can constrain a continuous, or otherwise very large set of numbers to a much smaller, discrete set by quantising it using a certain number of bits. This is an encoding step that maps numbers represented in one way into an equivalent representation that we can work on under a given FHE scheme.
At the time of writing, TFHE libraries (including the Concrete framework) are limited to quantising values using 8 bits. This limit applies to input and output values, and also to any accumulators that hold intermediary results during the process. The higher the quantisation bit width, the better the precision, and also the more expensive the calculations.
In our example, we specified that 5 bits are to be used for discretising the inputs, and only 2 (4 different values!) used for the weights within the model. The ‘Clear quantised model accuracy’ line in the above is a way of testing the accuracy of a model under the same parameter quantisation as in an actual FHE process, but without encrypting the values — in other words, it is a plaintext simulator for testing how quantisation affects model accuracy. As we can see in the above, the discretisation only lowered the test accuracy by 3.5%.
The ‘Homomorphic model accuracy’ is obtained from inference on test data actually encrypted using FHE. The accuracy is identical to that of the clear quantised model.
The overall drop in accuracy of the model run in FHE is still minimal when compared to the regular Sklearn logistic regression. This error would be reduced even further if a greater numbers of bits could be allocated for quantisation, and an increase in bit-width is an expected future development in Concrete.
However, despite the constraints, the above demonstrates the contemporary practicality of FHE: while staying well within a 8 bit limit, we are still able to achieve model accuracies comparable to operations on the plaintext.
Now we tackle a multiclass classification problem using the XGBoost model implemented by Concrete ML, based on Sklearn’s XGBoost implementation. This reflects another area where FHE sees great potential for deployment — Finance.
Financial data, whether it belongs to an organisation or an individual, also tends to be extremely confidential in nature. Finance is also a prime sector for the deployment of machine learning technology: hedge funds and trading firms may use market data to predict asset price trends; banks may use data collected on their customers to predict their likelihood of defaulting on a loan, and fintech companies may use its power to flag up fraudulent payments. It is easy to imagine the revolutionary benefits FHE could bring to finance by eliminating a huge portion of the risk and effort involved in maintaining data security and privacy.
This time, we’ll be shadowing the work of Roi Polanitzer in using multi-class classification for corporate credit ratings. The objective of the original work was to evaluate models that predict the likelihood of a company defaulting on a loan.
Here, we’ll be applying an XGBoost algorithm to the task of predicting defaults based on common financial metrics such as cost-to-income ratio.
Of course, in the real world this information is also highly sensitive; if this dataset were leaked, it could provide competing companies with insight into each other’s financial conditions. It would therefore need to be handled with the utmost care by the entity handling the loan, a requirement that is greatly enhanced by the ability to perform this computation over encrypted data.
We’ll be using the same dataset of corporate credit ratings as in the original article, which has kindly been provided here. As before, our associated Jupyter notebook for the full process can be found here. Again, we start with the necessary pre-analysis to determine the properties of the dataset.
# Import relevant libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# Load in Corporate Credit Rating dataset as a Pandas dataframe
df = pd.read_csv('ratings.csv')
# Visualise dataset
df.head()
# 'rating' is the response variable
Taking a peek at the layout of our data:
# Confirms that it is a balanced dataset df['rating'].value_counts() This verifies that there are 500 rows in the dataset for each of the 10 rating categories. We continue with data preprocessing, and performing a grid search, tuning the hyperparameters of the Sklearn model to optimise performance. We perform the same procedure on both the regular XGBoost by Sklearn, and Concrete ML’s implementation for its homomorphic equivalent. Here, we are using 4 bits for quantisation for the FHE model.
# Parameter grid used for GridSearchCV
param_grid = {
"max_depth": list(range(1, 5)),
"n_estimators": list(range(1, 201, 20)),
"learning_rate": [0.01, 0.1, 1],
"n_bits": [4] # 'n_bits' controls how many bits are used to quantise each value; generally more bits mean better accuracy, but slower to run
}
# We use shuffle split for cross validation
cv = ShuffleSplit(n_splits=5, test_size=0.3, random_state=0)
# Create a grid search variable and pass in the relevant arguments,
# then fit the variable with the training data
concrete_grid_search = GridSearchCV(
ConcreteXGBClassifier(), param_grid, cv=cv, scoring='roc_auc'
)
concrete_grid_search.fit(X_train, y_train)
# Set of optimal parameters for
concrete_best_params = concrete_grid_search.best_params_
# Now define the actual XGBoost model using optimised parameters
concrete_model = ConcreteXGBClassifier(**concrete_best_params)
# Training the actual model with the training data
concrete_model.fit(X_train, y_train)
# Compile the model to generate a FHE circuit
concrete_model.compile(X_train[100:])
# Generate an array containing the random permutation of integers in [0,49]
n_sample_to_test_fhe = 50
idx_test = np.random.choice(X_test.shape[0], n_sample_to_test_fhe, replace=False)
# This is so we can select a small random sample of size 'n_sample_to_test_fhe'
# in FHE, for a relatively quick test of model accuracy
X_test_fhe = X_test[idx_test]
y_test_fhe = y_test[idx_test]
# Train the same model from sklearn, and evaluate the accuracy
# The below procedure is the same as was done for the Concrete ML model
param_grid_sklearn = {
"max_depth": list(range(1, 5)),
"n_estimators": list(range(1, 201, 20)), # Tune the number of decision trees used in XGBoost. Default is 100
"learning_rate": [0.01, 0.1, 1],
"eval_metric": ["logloss"]
}
sklearn_grid_search = GridSearchCV(
SklearnXGBClassifier(), param_grid_sklearn, cv=cv, scoring='roc_auc'
).fit(X_train, y_train)
sklearn_best_params = sklearn_grid_search.best_params_
sklearn_model = SklearnXGBClassifier(**sklearn_best_params)
sklearn_model.fit(X_train, y_train)
y_pred_clear = sklearn_model.predict(X_test_fhe) # Regular plaintext prediction
y_pred_clear_q = concrete_model.predict(X_test_fhe) # Quantised plaintext prediction
y_preds_fhe = concrete_model.predict(X_test_fhe, execute_in_fhe=True) # FHE prediction
# Use Sklearn's built in accuracy evaluation function to compare accuracies of the different modes
from sklearn.metrics import accuracy_score
print(f'Accuracy score of clear model: {accuracy_score(y_test_fhe, y_pred_clear)}')
print(f'Accuracy score of clear quantised model: {accuracy_score(y_test_fhe, y_pred_clear_q)}')
print(f'Accuracy score of FHE model: {accuracy_score(y_test_fhe, y_preds_fhe)}')
# We expect the FHE accuracy to be equal to the quantised plaintext accuracy
Using 4 bits for quantisation, we achieved the following:
When the number of bits for quantisation is increased to 8, we get the following:
While 50–60% may not sound great (the original article saw around 80% accuracy for gradient boosting techniques), for a balanced dataset of 10 classes this is sufficiently accurate for our purposes in examining the performance of an FHE compatible XGBoost model built in Concrete.
We first note that the accuracy obtained from the clear model is different in both cases. Indeed, under the larger quantisation, the accuracy of the model drops.
The source of this behaviour comes from the use of a smaller testing set (Only 50 instances are chosen from the test set of 1667) — this is done so that the FHE model can run in reasonable time on conventional hardware. The regular XGBoost model is tested using the same small random sample to ensure fair comparison.
Using a larger training set would improve on this accuracy. Given the agreement between the clear model and the FHE model and the source of the accuracy issues, we would expect to achieve something similar to the original work in both cases. However, this would also require considerably faster processing if we wanted it in a practical time-frame. This is of course one of the many motivations for the work that Optalysys are doing.
As in the previous section, a specific result that is especially worth noting is the effect of quantisation bits on accuracy for the FHE model. With 4 bits, we saw a 20% decrease in accuracy of the FHE model compared to the unquantised model — from 58% down to 46%.
When we used 8 bits for quantisation, the FHE accuracy is exactly the same as the regular plaintext version (with a resolution of 2% of course, since only 50 data points are used in the test sample). Once again, there is no noticeable decrease between the quantised plaintext accuracy and that of actual FHE, a reassuring sign.
In both the above examples, the FHE implementations of machine learning algorithms used were based on the Scikit-learn’s API, which make it easy for data scientists or machine learning engineers who were familiar with the framework to get started with Concrete ML.
Concrete ML also has a PyTorch API — that enables models defined using PyTorch to be compiled into FHE circuits that can run inference on homomorphically encrypted data. Being a deep learning framework, the PyTorch API makes it easy to build well defined neural networks that also support FHE. Here we have a simple example that uses the Wine Classification dataset that is readily available from Scikit-learn. It contains 13 attributes on the levels of different chemicals’ presence in wine, and the target comprises 3 classes corresponding to 3 different wine cultivators in Italy, where it was collected.
# Importing relevant libraries
import numpy as np
import torch
from torch import nn
# Defining the neural network using PyTorch
# It has 2 hidden layers. Both hidden layers and the output layer have 3 neurones each
# The Sklearn wine dataset is a simple one to work with, so such a small neural network
# is already sufficient for achieving high accuracy
class NN(nn.Module):
def __init__(self, ip_size):
super().__init__()
self.linear1 = nn.Linear(ip_size, 3)
self.linear2 = nn.Linear(3,3)
self.linear3 = nn.Linear(3,3)
self.relu = nn.ReLU()
self.linear4 = nn.Linear(3,3)
def forward(self, x):
x = self.linear1(x)
x = self.relu(x)
x = self.linear2(x)
x = self.relu(x)
x = self.linear3(x)
x = self.relu(x)
x = self.linear4(x)
return x
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
# Load the wine dataset from Sklearn
X, y = load_wine(return_X_y=True)
# One Hot encoding the labels
y_encoded = []
for val in y:
if val == 0:
y_encoded.append([1,0,0])
if val == 1:
y_encoded.append([0,1,0])
if val == 2:
y_encoded.append([0,0,1])
y_encoded = np.array(y_encoded)
from sklearn.preprocessing import StandardScaler
# Standardising the values of the dataset for better accuracy
sc = StandardScaler()
X = sc.fit_transform(X)
# Splitting the features and the target into training and testing datasets
X_train, X_test, y_train, y_test = train_test_split(X, y_encoded, test_size=0.25, random_state=42)
X_train = torch.tensor(X_train, dtype=torch.float32)
X_test = torch.tensor(X_test, dtype=torch.float32)
y_train = torch.tensor(y_train, dtype=torch.float32)
y_test = torch.tensor(y_test, dtype=torch.float32)
# Initialising the model; defining the optimiser, the loss function and training hyperparameters
model = NN(X.shape[1])
criterion = nn.CrossEntropyLoss()
optimiser = torch.optim.SGD(model.parameters(), lr=0.1)
n_iters = 5000
batch_size = 50
# Training loop
for i in range(n_iters+1):
# Taking a random sample of size [batch_size] form X_train and y_train
idx = torch.randperm(X_train.size()[0])
X_batch = X_train[idx][:batch_size]
y_batch = y_train[idx][:batch_size]
# Making predictions, calculating the loss and optimising model parameters
y_pred = model(X_batch)
loss = criterion(y_pred, y_batch)
optimiser.zero_grad()
loss.backward()
optimiser.step()
if i % 100 == 0:
accuracy = torch.sum(torch.argmax(y_pred, dim=1) == torch.argmax(y_batch, dim=1)).item() / y_batch.size()[0]
print(f'Iterations: {i}\nAccuracy: {100*accuracy:.2f}%')
if accuracy == 1:
print('Training complete.')
break
The above code includes the definition and training of the simple PyTorch neural network.
Currently, FHE compatible neural networks can only be trained in plaintext. This is because of the huge amount of computation needed. In this case, because the network is quite small and the dataset is fairly straightforward, less than 300 iterations, each involving a batch size of 50, is needed before 100% accuracy is achieved on further training batches.
Modest neural networks used on more realistic datasets often require dozens of epochs with thousands of iterations per epoch before being trained properly. With the speed limitations of current FHE implementations and hardware, training directly in FHE would be unrealistic without Optalysys hardware, although there are certainly privacy use-cases where this would be desirable.
However, the spotlight for homomorphically encrypted machine learning is on encrypted inference — as real machine learning models can often either be trained using publicly available, or otherwise non-confidential, data, or make use of differential privacy and federated learning techniques to hide the training data.
Below, we compile the neural network into a FHE circuit, and compare its FHE test accuracy to its plaintext counterparts. 3 bits are used for quantisation.
from concrete.ml.torch.compile import compile_torch_model
# Compiling the model into a FHE circuit using Concrete ML
quantised_compiled_module = compile_torch_model(
model,
X_train,
n_bits = 3 # This is the quantisation bit width.
#In this case only 3 bits is sufficient.
)
X_train_np = X_train.numpy()
X_test_np = X_test.numpy()
y_train_np = y_train.numpy()
y_test_np = y_test.numpy()
unquantised_clear_predictions = model(X_test)
q_X_test_np = quantised_compiled_module.quantize_input(X_test_numpy)
quantised_clear_predictions = quantised_compiled_module(q_X_test_np)
from tqdm import tqdm
X_test_fhe = quantised_compiled_module.quantize_input(X_test_np) # Quantising the test dataset
quantised_homomorphic_predictions = []
# Iterating through the test sample, appending the quantising FHE predictions to the above list
for x_q in tqdm(X_test_fhe):
quantised_homomorphic_predictions.append(
quantised_compiled_module.forward_fhe.encrypt_run_decrypt(np.array([x_q]).astype(np.uint8))
)
# Dequantising the quantised FHE predictions
unquantised_homomorphic_predictions = quantised_compiled_module.dequantize_output(
np.array(quantised_homomorphic_predictions, dtype=np.int64).reshape(quantised_clear_predictions.shape)
)
# Comparing the accuracies for the different modes in which the model was ran
# (quantisation bit width: 3 bits)
acc_0 = 100 * (unquantised_clear_predictions.argmax(1) == y_test.argmax(1)).float().mean()
acc_1 = 100 * (quantised_clear_predictions.argmax(1) == y_test_np.argmax(1)).mean()
acc_2 = 100 * (unquantised_homomorphic_predictions.argmax(1) == y_test_np.argmax(1)).mean()
print(f"Test Accuracy: {acc_0:.2f}%") # Regular plaintext inference
print(f"Test Accuracy Quantized Inference: {acc_1:.2f}%") # Quantised plaintext inference
print(f"Test Accuracy Homomorphic Inference: {acc_2:.2f}%") # Inference using FHE
The resulting accuracies are as follows:
Despite being a small network, it is sufficient to achieve a very good accuracy of nearly 98% on the test set. The reason why only 3 bits are used for quantisation, is that the 8 bit limit applies also to the intermediary accumulators within the model, and the size of those intermediary values often greatly exceed those of the inputs. Therefore it is wise to choose a modest bit width, which in this case also achieved excellent results: the accuracy drop from regular inference to TFHE was about 4.5%, which still leaves the TFHE inference accuracy at above 93%; there is also no accuracy drop between the quantised plaintext inference result and that of the TFHE inference — showing that the large FHE ciphertexts perfectly preserved the integrity of the plaintext.
In the PyTorch example, we mentioned how the size of the intermediary values stored in accumulators while the neural network is running inference often greatly exceed that of the inputs. Here we will briefly look at the implications of this on TFHE, and the prospect of running larger deep learning models in TFHE in the future.
We are going to simulate a larger neural network for image classification, trained on the Fashion MNIST dataset, running in TFHE. Due to the size of the images — 728 pixels each — making the input size 728, the model is only capable of running inference in TFHE if 2 bits are used for quantising the inputs. This leads to an expectedly poor accuracy, of only 14%, down from a plaintext accuracy of nearly 90%.
Any larger bit width results in error, as some of the intermediary results end up requiring more than 8 bits to represent — exceeding TFHE’s current limit.
However, using the Virtual Lib tool from Concrete ML, we can simulate running the TFHE circuit in plaintext, with quantisation bit widths that exceeds the current limitations, and obtain results on how the accuracy, as well as how the maximum required accumulator size for storing intermediary values scales with the quantisation bit width.
This is important, as the future development pathway for TFHE incorporates higher bit precision. This tool thus aids understanding in the applications where TFHE will be useful in the future.
Below is the code and the results obtained;
# Importing relevant libraries and modules
import torch
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import torch.nn as nn
import torch.nn.functional as F
# Importing the Fashion MNIST Dataset as Pandas dataframes
training = pd.read_csv('fashion-mnist_train.csv')
testing = pd.read_csv('fashion-mnist_test.csv')
# Splitting the dataframes into X (features) and y (targets)
X_train, y_train = training.loc[:, training.columns != 'label'], training.loc[:, training.columns == 'label']
X_test, y_test = testing.loc[:, testing.columns != 'label'], testing.loc[:, testing.columns == 'label']
# Converting dataframes to NumPy arrays
X_train = X_train.to_numpy()
X_test = X_test.to_numpy()
y_train = y_train.to_numpy()
y_test = y_test.to_numpy()
# Normalising the X values by dividing by 255, as each feature is the value of a
# greyscale pixel, which is a number between 0 and 255 inclusive
X_train, X_test = X_train/255, X_test/255
# One Hot encoding the labels, transforming them from integer values (each representing)
# a category of clothing) to One Hot encoded binary arrays
from sklearn.preprocessing import OneHotEncoder
onehot_encoder = OneHotEncoder()
y_train = onehot_encoder.fit_transform(y_train).toarray()
y_test = onehot_encoder.fit_transform(y_test).toarray()
# Define a simple fully connected neural network using PyTorch
# It has a single hidden layer with 128 neurones, and an outpt layer of 10 neurones
# corresponding to the 10 different output classes
class FCNN(nn.Module):
def __init__(self, input_size):
super().__init__()
self.linear1 = nn.Linear(input_size, 128)
self.linear2 = nn.Linear(128, 10)
self.relu = nn.ReLU()
def forward(self, x):
x = self.linear1(x)
x = self.relu(x)
x = self.linear2(x)
return x
# Initialising the model with 728 input neurones; defining the optimiser
# and the loss functions
model = FCNN(X_train.shape[1])
learning_rate = 0.01
optimiser = torch.optim.Adam(model.parameters(), lr=learning_rate)
criterion = nn.CrossEntropyLoss()
n_epochs = 1
n_iters = 5001
batch_size = 50
# Training Loop
for epoch in range(n_epochs):
for i in range(n_iters):
# Taking a random sample of size [batch_size] form X_train and y_train
idx = torch.randperm(X_train.shape[0])[:batch_size].numpy()
X_batch = torch.tensor(X_train[idx][:batch_size]).type(torch.float32)
y_batch = torch.tensor(y_train[idx][:batch_size]).type(torch.float32)
y_pred = model(X_batch)
# Making predictions, calculating the loss and optimising model parameters
loss = criterion(y_pred, y_batch)
optimiser.zero_grad()
loss.backward()
optimiser.step()
if i % 1000 == 0 and i != 0:
_, predictions = torch.max(y_pred, 1)
_, labels = torch.max(y_batch, 1)
accuracy = predictions.eq(labels).sum() / batch_size * 100
print(f'Iteration: {i} | loss: {loss} |Accuracy: {accuracy}%')
print(f'Epoch {epoch+1} completed.')
# Evaluating the accuracy of the trained model on the test dataset
_, test_pred = torch.max(model(torch.tensor(X_test).type(torch.float32)),1)
_, test_labels = torch.max(torch.tensor(y_test), 1)
acc = test_pred.eq(test_labels).sum() / y_test.shape[0] * 100
print(f'Test Accuracy: {acc}%')
# Defining the configuration settings for testing the model using Virtual Lib
from concrete.numpy.compilation.configuration import Configuration
cfg = Configuration(
dump_artifacts_on_unexpected_failures=False,
enable_unsafe_features=True, # This is for our tests only, never use that in prod
)
# Taking a random sample of 100 from the test dataset, to test the accuracy
# using the Virtual Lib with a reasonable runtime
X_test_vl_idx = np.random.choice(X_test.shape[0],100)
X_test_vl = X_test[X_test_vl_idx,:]
y_test_vl = y_test[X_test_vl_idx,:]
# We are simulating (from 2 bits at the lower end) up to 16 quantisation bits
n_bits_max = 16
from concrete.ml.torch.compile import compile_torch_model
def test_with_concrete_virtual_lib(quantised_module, use_fhe, use_vl):
"""Tests the accuracy of the quantised model.
Passes in the compiled PyTorch model as argument, specify whether to run the
model in FHE or Virtual Lib.
Returns the accuracy of the test."""
# If we want to run the model in FHE, the inputs are cast to uint8
# But in this case we are merely simulating and don't want to limit ourselves
# to only 8 bits, so the inputs are cast to int32
dtype_inputs = np.uint8 if use_fhe else np.int32
all_y_pred = np.zeros((len(X_test_vl)), dtype=np.int32)
all_targets = np.zeros((len(X_test_vl)), dtype=np.int32)
# Two zero arrays the same length as the test sample are created
for i in range(len(X_test_vl)):
# Quantises one instance of the X test sample, for one iteration
sample_q = quantised_module.quantize_input(X_test_vl[i]).astype(dtype_inputs)
# Modifies one value (at index i) of the 'all_targets' zero array after each iteration
all_targets[i] = np.argmax(y_test_vl[i])
# Adds a dimension to the input
x_q = np.expand_dims(sample_q, 0)
# Either execute in FHE or simulated FHE, or simply quantised
if use_fhe or use_vl:
out_fhe = quantised_module.forward_fhe.encrypt_run_decrypt(x_q)
output = quantised_module.dequantize_output(out_fhe)
else:
output = quantised_module.forward_and_dequant(x_q)
all_y_pred[i] = np.argmax(output, 1)
n_correct = np.sum(all_targets == all_y_pred)
return n_correct / len(X_test_vl) # Returns the accuracy
accs = [] # List for storing accuracies for each different quantisation bit widths
accum_bits = [] # List for storing required maximum accumulator bit widths, for each quantisation bit width
# Loop for iteration over the range of quantisation bit widths that we want to test
for n_bits in range(2, n_bits_max+1):
print('{}'.format(n_bits)) # For debugging purposes
# Initalising the quantised PyTorch model using Concrete ML
q_module_vl = compile_torch_model(
model,
X_train,
n_bits=n_bits,
use_virtual_lib = True,
configuration=cfg,
)
# Appends the maximum acculumator bit width needed over each iteration to the list 'accum_bits'
accum_bits.append(q_module_vl.forward_fhe.graph.maximum_integer_bit_width())
# Appends the test accuracy over each iteration to the list 'accs'
accs.append(
test_with_concrete_virtual_lib(
q_module_vl,
use_fhe=False,
use_vl=True,
)
)
# Plots the accuracy and maximum accumulator bit width (currently incorrect)
# over the range of quantisation bit widths, and displays the plot
fig = plt.figure(figsize=(12, 8))
plt.rcParams["font.size"] = 14
plt.plot(range(2, 2+len(accs)), accs, "-x")
for bits, acc, accum in zip(range(2, 2+len(accs)), accs, accum_bits):
plt.gca().annotate(str(accum), (bits - 0.1, acc + 0.025))
plt.ylabel("Accuracy on test set")
plt.xlabel("Weight & activation quantization")
plt.grid(True)
plt.title("Accuracy for varying quantization bit width")
plt.show()
The result obtained is shown below:
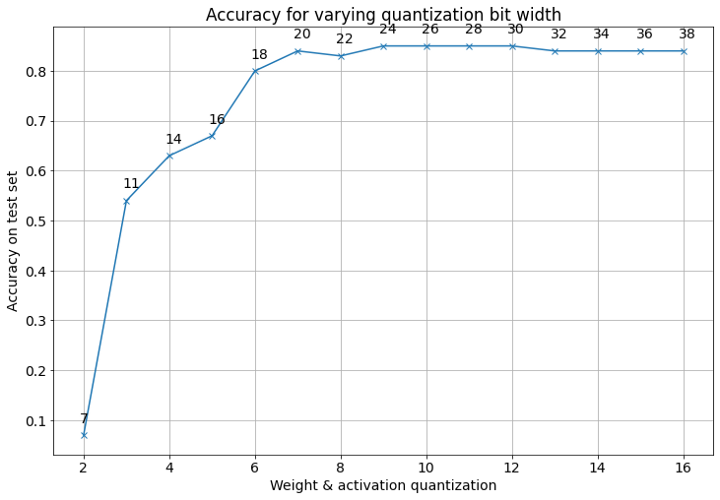
The plaintext model has an accuracy of 86.4% in this case. As the quantisation bit width (shown on the X-axis) increases, the simulated TFHE model accuracy on the test set (y-axis) increases in a logarithmic growth pattern. We see that from 7 to 8 bits upwards, the quantised model accuracy approaches the asymptote that is the actual model accuracy — which uses 32 bit floating point representations. This shows that excessive accuracy is often not necessary for image recognition, and demonstrates the suitability of TFHE for similar deep learning applications.
The small numbers annotating each datapoint are the maximum accumulator bit widths — in other words, what the upper bit width limit for representing values in TFHE must be, for us to be able to run the model at that precision. We see that they greatly exceed the quantisation bit widths by orders of magnitude. It is not hard to see why: in this case we have 728 inputs, and therefore the neurons in the hidden layer would need to represent the sum of 728 values. The current limitation of 8 bits is too low, but this limit is bound to increase in the future, especially as better hardware for FHE becomes available.
The above examples illustrates that in principle — machine learning can be combined with FHE with astounding ease. Having spent most of its lifetime confined to esoteric research papers done by highly specialised experts, recent open source FHE libraries such as Concrete, are testament to this technology becoming ever more accessible to the masses. Using simple APIs as demonstrated in this article, data scientists and machine learning engineers with no prior knowledge of cryptography can very easily transpile statistical analysis/machine learning models into FHE compatible equivalents. We also bear in mind that Concrete ML is still in its alpha stages of development.
Of course, the current limitations of TFHE are also evident. The current 8 bit limitation of the Concrete library meant that the level of homomorphically encrypted machine learning available currently is restricted to simple models on relatively easy datasets. The loss of accuracy due to quantisation — from having to abide by this limit — is also a concern for slightly larger models.
However, in practice such ‘simple’ models are used in many, if not most, practical applications of Machine Learning. While very large models like GPT-3, Dall-E, and Stable Diffusion grab headlines by demonstrating features which were until recently firmly in the realm of science fiction, Machine Learning is also extensively used in Health Sciences, Finance, and Engineering to solve smaller, but high-value, problems for which a logistic regression, tree-based approach, or a very small neural network, is the perfect tool. (This is especially the case when the amount of available training data is small.) As we demonstrate above, FHE already provides results which are close or identical to those of non-encrypted models in these cases.
In order to look at the future potential of FHE, we must look at the root cause of its remaining limitations — the fact that conventional computing hardware is simply not optimised for the specialised type of computation necessary to run FHE. This is due to the nature of the ciphertexts used in most modern FHE schemes, where values are represented by huge vectors containing the coefficients of large polynomials. The number of multiplications involved when multiplying two such ciphertexts together — a very common operation — would result in an unreasonably large number of calculations that would be very slow on most modern computing hardware.
As a result, modern FHE libraries use Fourier or Number-Theoretic Transforms to convert these ciphertexts into a form that is easier to multiply — but this is still extremely slow using most conventional electronics. Hence the main drawback of current FHE technology — speed; the same calculations performed on fully homomorphically encrypted data take up to a million times longer compared to plaintext. This also explains the limitations on precision for Concrete ML: any more bits, and the calculations would become unacceptably slow.
In order to level up the scale at which FHE can be deployed, we need better hardware specialised for FHE, and this is where companies like Optalysys come in.
Optalysys has the key to unlocking the power of FHE, by leveraging the power of physical phenomena using optical computing. Existing optical modulators are capable of encoding data into light, and operate in a ultra-fast timeframe greatly exceeding that of conventional integrated circuits. Under the right conditions, light will instantaneously perform a Fourier Transform on the data encoded into it by undergoing the natural phenomenon of diffraction. By constructing optical circuits on silicon, and integrating with conventional integrated circuits specifically designed to work natively with FHE ciphertexts, we can make use of this remarkable natural phenomenon, to compute the vast quantities of Fourier Transforms and related operations (such as Number-Theoretic Transforms) required for FHE operations at a rate that conventional accelerators such as FPGAs can’t hope to match.
As mentioned previously, the technology of FHE is considered to be the Holy Grail of cryptography, for the revolutionary impacts it would yield for cybersecurity, effectively eliminating the risk posed by data theft. In a world where rapid advances in fields such as cloud computing and AI often seem to be at odds with privacy and confidentiality, FHE holds the potential to reconcile this conflict — enabling businesses and consumers to take advantage of the benefits of technologies such as machine learning, whilst ensuring their data remains more secure than ever.
Breast Cancer Dataset
News
© 2024 All rights reserved Optalysys Ltd
Subscribe
Sign up with your email address to receive news and updates from Optalysys.
