The size and complexity of AI models is vastly outpacing the rate at which baseline computing performance is growing. If we are to make use of mass-scale AI in the future, the solutions are stark: use exponentially more power on general-purpose hardware, or reach for more efficient and specialised hardware in the form of AI accelerators.
The idea of dedicated hardware for a specific task isn’t new. The sheer number of operations per second (OPS) required to process high resolution computer graphics has been outstripping the capabilities of digital systems since the 1970s.
For deep learning purposes, the specialist hardware has its roots in the late 1990s. At the time, graphics were becoming increasingly complex but general-purpose CPUs couldn’t keep up. While many of the calculations required for rendering graphics are relatively simple, the challenge lay in executing many of these instructions simultaneously on a large amount of data.
Over time, it made sense to develop a co-processor, a separate piece of hardware designed specifically to perform these calculations, to take the load off the CPU. A new architecture was envisaged, with very different requirements to the traditional CPU: what was needed was something that can do a single instruction on multiple data simultaneously (known as the SIMD architecture).
The piece of hardware designed for this task, known as a Graphics Processing Unit (or GPU), is specialised for SIMD, and has a much higher throughput on such tasks. However, the SIMD paradigm doesn’t just apply to graphics acceleration; any application where the same instruction needs to be carried out in parallel on lots of data can be accelerated in this way. And that is why the GPU went on to become a major driver of the AI revolution.
The utility of GPUs in this field was twofold:
The way they performed many calculations in parallel
The fact that AI models use simple operations, with a single instruction applied to a batch of data (SIMD).
AI may be constantly breaking new ground, but at its core the vast majority of the calculations performed (additions and multiplications) have not changed; GPUs were the most efficient “ready-made” hardware for doing these calculations. However, in many cases, the calculation requirements of AI are even simpler than the limited range of operations that GPUs can perform. As research in AI has developed, we’ve also seen a shift away from the kind of high-precision numbers that are required for most mathematical calculations towards lower precision; it’s estimated that just 4-bit representations are sufficient for high accuracy on machine vision tasks.
By designing ever more specialised hardware that performs an increasingly limited range of computations, hardware manufacturers have thus so far been able to dodge the core issue: even if it maintains the exponential trajectory it is famous for, Moore’s law is no longer meeting requirements for heavier computing tasks.
This move to specialism has led to some exceptionally efficient hardware. The typical metric for assessing the performance of an AI accelerator is now in units of trillions or “Tera”-operations per second (TOPS), and as power efficiency is often critical (such as in edge applications) then the current standard for measuring performance is in the TOPS per Watt.
However, the measure of TOPS has a well-known problem; it doesn’t give you an idea of the kind of operations that the system is performing, nor does it give you a good measure of how well the system will perform on specific tasks.
For AI, one of the most important calculations is known as a Multiply-and-Accumulate (MAC). It’s an extremely simple operation; multiply two numbers, and then add the result to an accumulator, a register that stores a value. Despite their simplicity, MACs are critical for performing the kind of matrix-vector operations that form the core of most machine learning algorithms. One individual MAC represents 2 operations, so to tie TOPS and MACs together, one TOP=0.5 TMAC, another common unit of accelerator performance.
Here’s a diagram showing the usual flow of information for the convolution of an input array with a bank of kernels, known as a multi-channel convolution, a critical part of most machine vision applications.
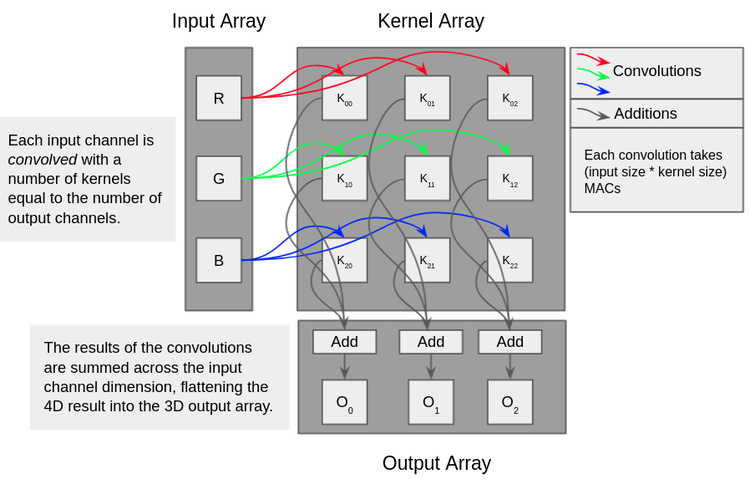
In a typical convolutional network, input channels (such as the red, green and blue channels from an image) are multiplied with kernel arrays.
And here’s an animation showing how many parallel operations that this translates into for a single small input channel. You can see that despite the small size of the kernel and the channel, the number of MAC operations is a product of input size and kernel size.
That’s for a single input channel with a single kernel, just one of the multiplication operations shown in the diagram above. Now consider the size and scale of the input channels and kernels in a modern computer vision AI network, and then multiply that by the number of inferences or training steps that might be required.
Suddenly, a trillion operations (500,000,000 MACs) per second starts to look like it might not be enough, and indeed it isn’t; individual modern GPUs and deep learning accelerators are advertised as performing anywhere between ~4 TOPS for highly-efficient edge processors all the way up to ~624 TOPS at the very top end (although how you define this depends on a host of factors, such as numerical precision). However, the importance of MACs isn’t a new thing; amongst the many things they’ve been used for over the decades is in the field of digital signal processing, or DSP.
One of the best-known tasks in DSP is the Fourier transform, and MACs are also a key part of calculating the digital implementation, the Fast Fourier Transform (FFT) algorithm.
This is important from a deep learning perspective, because when it comes to convolutional neural networks, Fourier transforms (FTs) can yield major improvements in efficiency. Using a Fourier transform, the number of operations in the convolution operation becomes linear rather than quadratic, leading to a vast reduction in operations required.
This algorithmic benefit is usually not realised in the real world due to the lack of hardware efficiency when calculating the FT vs. performing simple MACs. The Fourier transform itself requires complex exponents which are not a simple operation at all, requiring 100s of clock cycles. Furthermore the FFT itself is not a linear operation, leading to a worse-than linear algorithm from end to end.
So how do the benefits of optical computing translate to AI? We know on the surface that it’s fast; after all, light is the fastest thing in the universe. But what can get lost in translation are the reasons why it is fast.
There are two ways in which to make any task which involves multiple steps faster. You either perform the individual steps in less time, or you reduce the total number of steps.
Consider the Fourier transform; the number of operations required for the “naive” way of solving a discrete Fourier transform scales as O(n²), whereas the Fast Fourier transform scales as O(n log (n)). Both algorithms achieve the same outcome, but for practical purposes the FFT is always faster for non-trivial datasets because it fundamentally involves fewer steps.
In a world in which TOPS and TMACS are a dominant measure of performance, the usual way to accelerate a process is to increase the rate at which you can perform these calculations. Maybe you make increased use of parallelism, boost the clock speed of your processing core, or even make use of optical technology to perform MAC operations. All of these approaches look different, but they are all pursuing an increase in overall OPS.
But with Fourier optics, we are not solely trying to increase the rate of OPS; we’re shifting the data into a format which is fundamentally easier to deal with, albeit without the usual overhead cost that comes with electronic techniques. There are two ways of looking at the benefits of our approach.
The first (from a conventional DSP perspective) is that an enormous number of MACs and complex exponents are being performed instantaneously, and the log(n) steps required to wait for a FFT algorithm (even on infinitely parallelised hardware) are entirely removed.
But the second perspective makes the utility even more apparent. When viewed from the perspective of a digital system performing convolution tasks, we can look at it in the same way as the algorithmic improvement that comes from switching from the “naive” discrete-FT to the FFT; there’s simply fewer MACs involved.
With respect to AI, a unique benefit of the Fourier-optical method is that, in practical terms, it reduces the overall number of MACs that need to be performed when executing convolutions. And these reduced MACs can still be performed on any processor, optical or otherwise.
Here’s a diagram of how our Fourier-optical processor fits into the information flow for convolutions:
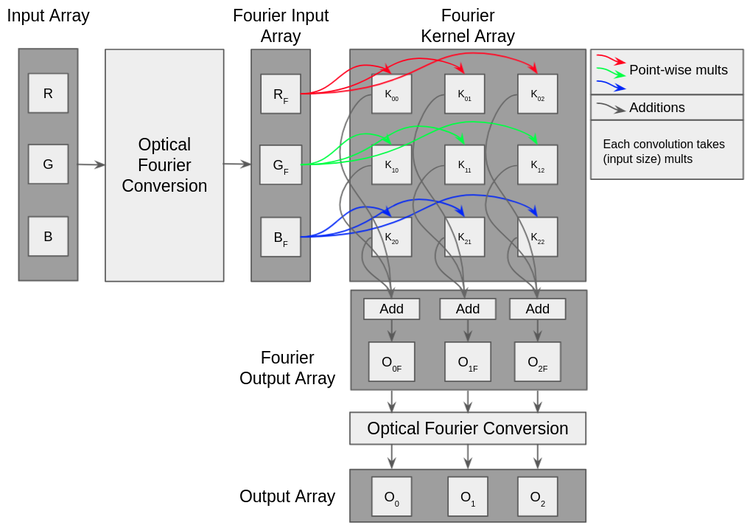
And here’s the effect that this has on the number of GEMM operations that have to be performed on the GPU
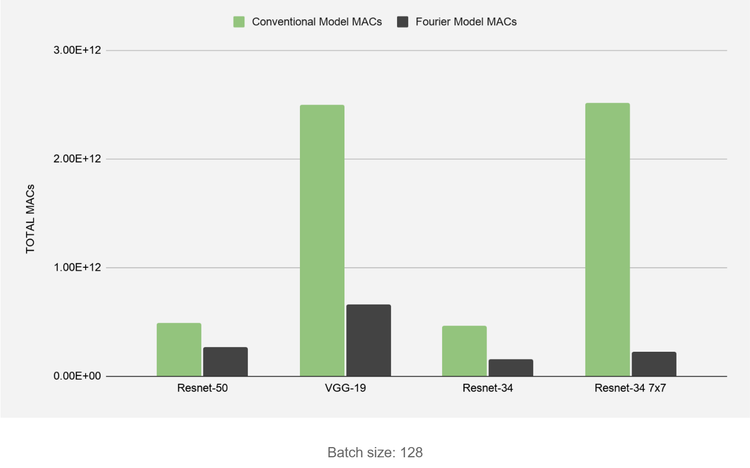
The impact this can have on CNN acceleration is exceptional; we outline the reduction in the total number of discrete MACs required for various convolutional networks in the following bar chart, which shows the total reduction in operations for the entire network, not just the convolutional layers. We stress that these networks can still be processed on any conventional electronic hardware like a GPU, but with far fewer operations required for the same maths to happen. This means that more channels in a convolutional network can be processed in parallel on the GPU, without having to make the GPU itself any faster.
The most significant gains can be seen for model architectures that make greater use of convolutions with filters larger than 1 pixel (like VGG-19) but even Resnet-50, where only around 40% of layers can have their MAC count reduced by our method, still enjoys a significant reduction in the number of required operations. The larger the kernels used in the convolutional layers, the greater the reduction in MACs.
As long as the optical system can keep pace with the speed at which information is transferred to and from an auxiliary processor, this effect holds true regardless of the peak speed of the optical system! This has knock-on benefits which, as far as we can tell, are entirely unique to this approach.
The single most important one of these is that, because this form of acceleration can be considered to be entirely separate to the usual “more MACs in the same time” approach to acceleration, then the Fourier-optical approach can further accelerate any other AI accelerator system as a complementary technology.
This wholly different perspective on acceleration and the way in which optical “MAC reducing” hardware works hand-in-hand with digital or optical “faster MACs” hardware leads us to identify the technology as a second-order AI accelerator due to the quadratic improvement in convolution performance that it can confer on any other system.
It bears repeating that these benefits are entirely separate from the advantages that come from the ability to use ultra-fast optical components. Silicon photonics allows us to punch through existing limits on the Ops front too; individual modulators with data rates of up to 50 Gbps already exist, and the technology offers the ability to push processing way beyond what is possible with conventional electronics.
However, when used in the role of an accelerator for AI models and other convolutional tasks, the technology isn’t reliant on reaching the very upper limits of performance with respect to speed. Even in a model of computing which is still constrained by interface speed and the Von Neumann architecture, the Fourier-optical method is perfectly capable of delivering improvements in performance from the word go.
News
© 2024 All rights reserved Optalysys Ltd
Subscribe
Sign up with your email address to receive news and updates from Optalysys.
