In this article, we show how to compute the maximum and minimum of an encrypted array of data without decrypting it, using Zama’s Concrete implementation of the TFHE programmable bootstrapping. We then use this ability to design a sorting algorithm which can work on encrypted data. Finally, we comment on the potential for optical acceleration, showing that Optalysys technology can accelerate the main bottleneck by more than 100
Fully Homomorphic Encryption (FHE) allows for arbitrary calculations to be performed on encrypted data, thus removing the need to decrypt it for analysis. In principle this closes the last remaining gap in data security: using previous forms of encryption, data may only be encrypted when at rest (e.g on a hard drive) or in transit (such as passing through the internet). FHE is the only generalisable approach for protecting data in use.
However, FHE currently suffers from two major issues that hinder its commercial viability. The first one is speed: calculations on encrypted data can be thousands to millions of times slower than what can be achieved on plaintext data. The second is the domain knowledge needed to implement and work with FHE schemes efficiently.
Fortunately, rapid progress has been made in the years following Craig Gentry’s seminal thesis where the first FHE scheme was proposed. Two recent advances are Zama’s Concrete library, and the C++ transpiler written by the Google FHE team.
Google’s C++ transpiler is a tool to convert regular C++ code into TFHE code via an XLS intermediate representation generated by XLS[cc], making it straightforward to convert existing code for use in FHE (with some limitations) without expert knowledge of the field.
Zama’s Concrete library is also built on TFHE and uses programmable bootstrapping to perform any univariate operation in a single bootstrap. This can significantly reduce the number of operations which needs to be performed during tasks such as encrypted deep learning inference. It also provides high-level functions for homomorphic operations; these include such things as the addition of two ciphertexts, multiplication by a plaintext, multiplication of two ciphers, or programmable bootstrapping. Concrete not only supports these operations but also provides several sets of default parameters, allowing non-cryptographer developers to start working quickly and safely with FHE. (See the documentation for more details.)
Concrete has already been used to demonstrate several applications with both industrial and academic interest; over the course of testing our optical processing hardware design, we’ve performed many of our own demonstrations in tasks such as recurrent neural network inference, Conway’s game of Life, and encrypted string search.
In this tutorial, we’ll add to these previous efforts by demonstrating how to use Concrete to homomorphically compute the maximum or the minimum values in an encrypted array, without needing access to the plaintext data. Computing maxima and minima can be used, for instance, to sort arrays or to implement certain pooling layers in Deep Learning. We give an example of the former at the end of the tutorial.
At Optalysys, we are developing optical computing chips that can accelerate the main components of FHE calculations. These tutorials come about in part as an outcome of our efforts to better understand the requirements of this technology. We aim to develop a solution that not only works for FHE, but works as well as possible.
Beyond this, we also understand the value of working with the community to ensure that FHE continues to develop into a tool which is as user-friendly as possible. This is especially important given that FHE touches upon deeper aspects of the application space in a way that other uses of encryption generally do not. With this expansion in capabilities comes a corresponding degree of complexity, and it is essential to the success of FHE that developers, data scientists and other specialists have the resources to help them build the applications of tomorrow.
Of course, understanding is only half the problem; reaching the stage where that knowledge can be applied requires a massive jump in the speed at which FHE schemes can be executed, and that is the other focus of this article. At Optalysys, we are designing technology that can accelerate the primary bottleneck in FHE operations by a factor 100, and we have our focus set on even higher accelerations in the future.
The key to tackling this problem lies in the same mathematical function that our technology was originally designed to conquer: The Fourier transform. This mathematical tool finds uses in every technical discipline, but it is especially important for FHE.
At the heart of calculations in FHE is the need to multiply very large polynomials together, a task which is considerably easier when executed in Fourier space. This is both well known and well understood, and contemporary FHE schemes executed in electronics already use fast Fourier transform algorithms to make these multiplications easier.
However, the electronic algorithm comes at the cost of many repeated operations that cannot be run entirely in parallel; when massive volumes of Fourier transforms are required, this inevitably leads to additional time spent on the calculation. In the case of FHE, up to 90% of all the computational load is currently occupied solely by Fourier transform calculations, and that number is expected to grow.
We take a different approach; we manipulate the properties of optics to perform Fourier transforms at nearly the speed of light. Our technology is a highly scalable optical computer that can be integrated into existing digital systems.
This unique approach to calculating the Fourier transform has come about at exactly the right moment to provide acceleration for FHE. In this article, we combine our existing system simulators and interfaces with Zama’s Concrete FHE library to get a sense of just how powerful the first generation of our systems will be at tackling one of the most pressing issues in the digital world.
Generally speaking (at least with respect to FHE), there are two different ways to perform computations on encrypted data. The first, which we’ve used extensively in our previous articles, is to express tasks as a sequence of logical operations. In this case, the processes we want to apply to a piece of information are converted into a representation in terms of unary and binary boolean gates; these gate operations on the data can then be evaluated homomorphically. Two very good tools for this are the Google C++ transpiler and the Concrete Boolean library.
The second approach, which we will follow here, is to work directly with integers or continuous numbers (to within some level of accuracy) and use the operations provided by a given FHE scheme to reconstruct a desired function. Depending on how we go about things, this approach can be much faster than attempting to do the same operation via homomorphic-Boolean logic. In this article, we’ll apply this approach to the task of computing the maximum and minimum values of an array of numbers using only additions and univariate functions. We will again use the Concrete library, which makes this task much easier.
Before heading into our implementation, we’ll briefly explain our thinking with unencrypted examples. Given two numbers a and b:

Our objective is to find their maximum using only additions, or functions which take only one argument. One possibility for finding the maximum value is the following:

2. Compute the sum d = b + c.

3. Define the positive part e of d: e = d if d > 0 and e = 0 otherwise (here, e=0).
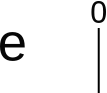

We can perform a similar trick to find the minimum:


This approach takes advantage of the speed benefit that we described above; in FHE, additions and multiplication by a constant (here, -1*a) are typically fast (although not as fast as their plaintext counterparts) because they do not require a bootstrap afterwards. In each of these two algorithms, there is thus only one “slow” operation requiring a bootstrap: taking the positive or negative part of d.
Once you can compute the minimum and maximum of two numbers, it is easy to compute the maximum and minimum values of a larger set by doing multiple comparisons of pairs of entries. For a set of N elements, this requires N-1 comparisons.
Homomorphic version
Let us now illustrate this on a larger set. Consider an array of numbers representing a discretised sine function:
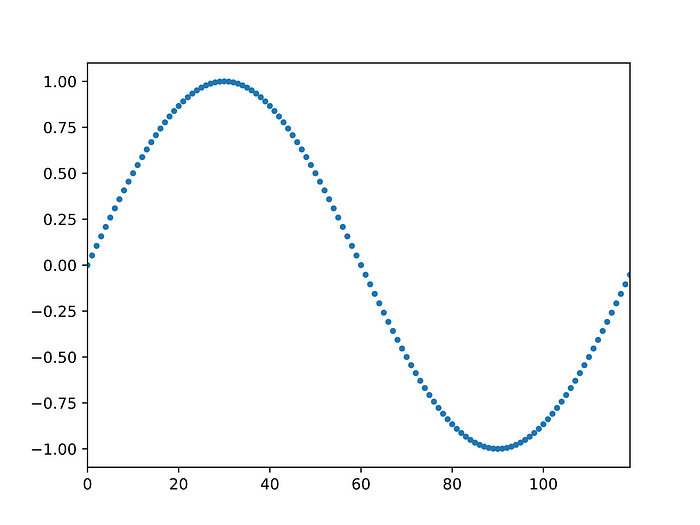
In this figure, it is easy to see that the maximum is 1 and the minimum is -1:
The catch, or course, is that we can’t send this array directly to the server — the point of FHE is that the server where computations are performed does not need access to the plaintext data. Instead, we first encrypt the data before sending it to the server. Each element of the array thus becomes a vector of real values. This vector can be converted to a single number, but this one will have no relation to the original value. On encryption, the array now looks essentially random:
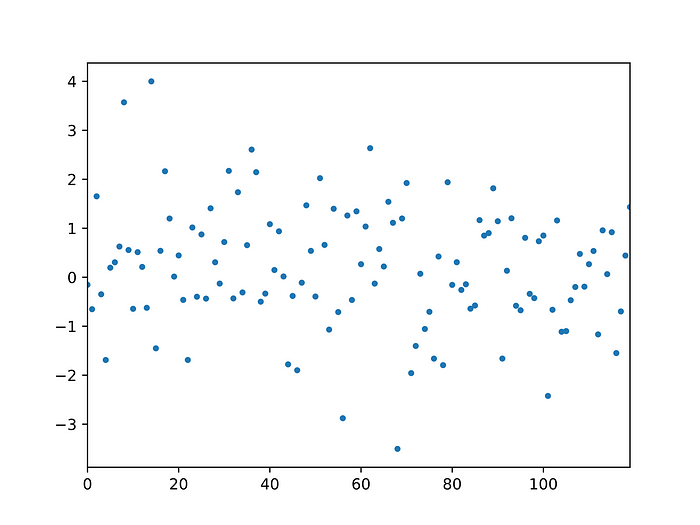
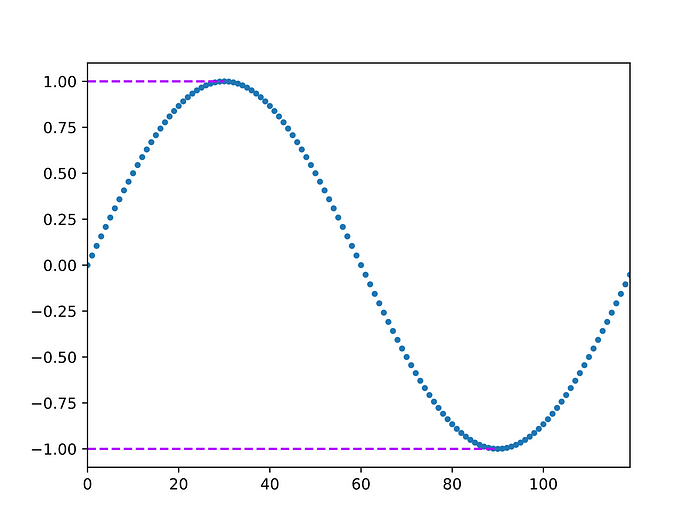
The advantage of this is obvious: since the data looks random (in fact it doesn’t just look random: it can be shown that, without the secret key, it is indeed indistinguishable from random noise), it can be safely sent without risk of data leak. In the following, we will show how we can nonetheless recover the maximum and minimum in encrypted form, as schematically illustrated in the next figure:
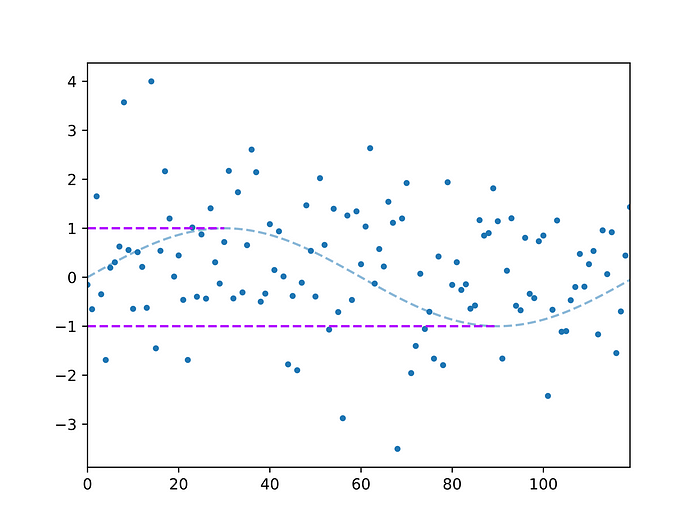
Here, the dashed lines represent plaintext data; none of these is available to the server. The latter only has access to encrypted data, represented by the blue dots. What we will show is how, using programmable bootstrapping and other FHE operations, we can generate two new ciphers which, when decrypted by the client, give the maximum and minimum of the original array (purple dashed lines).
Preliminaries
To run the code in this tutorial, you will need a Rust compiler (instructions to install one can be found on the rust-lang website). Run cargo new --lib homomorphic_min_max to create a new Cargo project. Since we use Concrete, you will also need to add it as a dependency by adding concrete = "0.1.11" in the [dependencies] section of the Cargo.toml file.
Unless said otherwise, the code shown below can go in the src/lib.rs file, which should start with use concrete::*; . This places Concrete’s structures and functions in the current namespace.
In the following, we will go through the code step by step, explaining as we go. A full version of the code is available in the Appendix.
In the following, we start by creating functions that use Concrete to cryptographically compute the same sequence of steps that we demonstrated on the unencrypted example. We then take these functions and show how we can apply them to arrays of encrypted values, allowing us to find the maximum and minimum values in these arrays without needing to decrypt the information!
Max algorithm
The first thing we need is the function to compute the maximum of two encrypted values. We can’t just compare the ciphertexts — since a ciphertext should not leak any information about the message it encrypts, there is no way to see which one encrypts the larger value without the decryption key. Instead, we will use Concrete to construct the sequence of additions, comparisons and subtractions used to check for the maximum value, and then generate a new ciphertext which is a (different) encryption of the largest value:
fn compute_max(cipher_1: &LWE, cipher_2: &LWE, ksk: &LWEKSK, bsk: &LWEBSK,
encoder: &Encoder, zero: &LWE)
-> Result<LWE, CryptoAPIError>
{
// difference between the two ciphers
let cipher_diff = cipher_2.add_centered(&cipher_1.opposite()?)?;
// programmable bootstrap to check if the difference is positive
let mut cipher_diff_pos = cipher_diff.bootstrap_with_function(bsk,
|x| if x >= 0. { x } else { 0. },
encoder)?;
// change the key back to the original one
cipher_diff_pos = cipher_diff_pos.keyswitch(ksk)?;
// add the result to cipher_1
let mut result = cipher_1.add_centered(&cipher_diff_pos)?;
// subtract 0 to reset the encoder offset
result.add_centered_inplace(zero)?;
Ok(result)
}
This function takes six arguments:
cipher_1 and cipher_2 are two ciphertexts encrypted with the LWE version of TFHE. They encrypt the two values we want to compare.ksk is a key-switching key: a public key (by ‘public’, we mean that this key can be safely shared as it can not reveal any information on the messages) which can convert a cipher encrypting a message m with one key to a different cipher encrypting the same message with a different key. It is needed because the programmable bootstrap will generally change the encryption key; the key-switching key is used to revert to the original one.bsk is the bootstrapping key, required to perform the programmable bootstrap. Like ksk, it is a public key.encoder is, as its name indicates, an encoder, used to map floating-point values to a fixed set of values that the encryption and decryption schemes can work with and back. Strictly speaking, this parameter is not really needed: we could use the same encoder as that of cipher_1 or cipher_2. However, we prefer to include it as an explicit argument to give the function more flexibility, as choosing a different encoder may improve the accuracy in some cases.zero is an encryption of the value 0 with a carefully chosen encoder to cancel the drift. Indeed, even if cipher_1 and cipher_2 have the same encoder, performing homomorphic operations will generally change it. This is not a problem when comparing only two numbers as the final encoder will always be able to represent the result (assuming cipher_1 and cipher_2 are correctly encoded). However, it may become an issue if this result is then compared with other values. Adding an encryption of 0 with the right encoder cancels this effect, and ensures the output of the function can be compared with other values.Let us go through how this function works line by line:
let mut cipher_diff_pos = cipher_diff.bootstrap_with_function(bsk,
|x| if x >= 0. { x } else { 0. },
encoder)?;
computes the positive part using programmable bootstrapping thanks to the bootstrapping key bsk, a closure computing the positive part of a floating-point number (|x| if x >= 0. { x } else { 0. }), and the encoder passed to the function. At this point, cipher_diff_pos is an encryption of the result, but under a different key than the original.
cipher_diff_pos = cipher_diff_pos.keyswitch(ksk)?;
The above then switches the encryption key back to the original one held by the sender. The line
let mut result = cipher_1.add_centered(&cipher_diff_pos)?;
then computes the sum of the result and cipher_1. The operation
result.add_centered_inplace(zero)?;
adds an encryption of 0, which has the effect of re-centering the encoder.
Finally, the function returns a Result containing either a ciphertext if all operations were successful, or a CryptoAPIError (an error type defined by Concrete) if one of them failed.
NB: Technically, the key-switching step is not absolutely necessary: we could also choose the input and output keys of the bootstrapping operation to be the same, and thus not need to change the key afterward. In this article, we choose the input and output keys independently to illustrate a very useful property in Concrete, since the runtime overhead of the key switching is quite small in practice.
Min algorithm
The function to compute the minimum of two values is very similar, and proceeds along the same lines as the maximum function:
fn compute_min(cipher_1: &LWE, cipher_2: &LWE, ksk: &LWEKSK, bsk: &LWEBSK,
encoder: &Encoder, zero: &LWE)
-> Result<LWE, CryptoAPIError>
{
// difference between the two ciphers
let cipher_diff = cipher_2.add_centered(&cipher_1.opposite()?)?;
// programmable bootstrap to check if the difference is positive
let mut cipher_diff_pos = cipher_diff.bootstrap_with_function(bsk,
|x| if x >= 0. { x } else { 0. },
encoder)?;
// change the key back to the original one
cipher_diff_pos = cipher_diff_pos.keyswitch(ksk)?;
// subtract the result from cipher_2
let mut result = cipher_2.add_centered(&cipher_diff_pos.opposite()?)?;
// add 0 to reset the encoder offset
result.add_centered_inplace(zero)?;
Ok(result)
}
The primary difference is that we add the opposite of the positive part of the difference to cipher_2 instead of directly adding the positive part to cipher_1.
Maximum
We can now use the function compute_max above to compute (an encryption of) the maximum of an array of numbers:
pub fn compute_max_array(ciphers: &[LWE], ksk: &LWEKSK, bsk: &LWEBSK, encoder: &Encoder, zero: &LWE)
-> Result<LWE, Box<dyn std::error::Error>>
{
// compute the opposite of 0 to reverse the encoder
let zero = zero.opposite()?;
// convert the array of ciphers into an iterator
let mut ciphers_iter = ciphers.iter();
// set the result to the first cipher, or return an error if the iterator is empty
let mut result = ciphers_iter.next().ok_or("Empty cipher array!".to_string())?.clone();
// loop over the other ciphers
for cipher in ciphers_iter {
// get the maximum of the current result and next cipher
result = compute_max(&result, cipher, ksk, bsk, encoder, &zero)?;
}
Ok(result)
}
We make this function public (pub) so that it can be accessed from other files. Its arguments are similar to those discussed above except for the first one, ciphers, which is an array of ciphertexts.
The first line of this function may be surprising at first sight: it computes the opposite (in encrypted form) of 0. Of course, this operation will not change the value obtained after decryption (since -0 = 0). But it will change the encoder of the ciphertext.
This is one of those rare moments where we have to be aware of how Concrete works on a deeper level; if zero originally has the same encoder as the elements of ciphers, then the new cipher obtained after taking the opposite has just the right encoder to cancel the drift that compute_max would otherwise entail.
The rest of the function follows quite standard coding practice: we convert the array to an iterator, set the result to its first elements (or raise an error if the array is empty), then loop over the other elements to find the global maximum.
Minimum
As before, the function used to compute the minimum of an array is very similar:
pub fn compute_min_array(ciphers: &[LWE], ksk: &LWEKSK, bsk: &LWEBSK, encoder: &Encoder, zero: &LWE)
-> Result<LWE, Box<dyn std::error::Error>>
{
// convert the array of ciphers into an iterator
let mut ciphers_iter = ciphers.iter();
// set the result to the first cipher, or return an error if the iterator is empty
let mut result = ciphers_iter.next().ok_or("Empty cipher array!".to_string())?.clone();
// loop over the other ciphers
for cipher in ciphers_iter {
// get the minimum of the current result and next cipher
result = compute_min(&result, cipher, ksk, bsk, encoder, &zero)?;
}
Ok(result)
}
The only differences between this and the maximum array iterator are that we don’t need to take the opposite of 0 and, of course, that we are using ourcompute_min function instead of compute_max.
Example
Let us show how to use these functions on a simple example. Create a file src/main.rs containing
use homomorphic_min_max::*;
fn main() -> Result<(), Box<dyn std::error::Error>> {
}
The code shown in the rest of this section should go in this main function.
We first define the encoder. We will work with values between 0 and 1, with 4 bits of accuracy. We set the number of bits of padding to 2. (See the concrete documentation for more information on the encoders, keys, and parameters.)
// secret keys
//
// polynomial size: 1024
// security level: 128 bits
let sk_rlwe = RLWESecretKey::new(&RLWE128_1024_1);
let sk_in = LWESecretKey::new(&LWE128_1024);
let sk_out = sk_rlwe.to_lwe_secret_key();
We then define the key-switching key, needed to convert a ciphertext for the key sk_out to a ciphertext for sk_in, and the bootstrapping key. They both take two parameters, which we set to 5. (See the Concrete documentation.)
// define the key-changing key and bootstrapping key
//
// base log: 2^5
// number of levels: 2^5
let ksk = LWEKSK::new(&sk_out, &sk_in, 5, 5);
let bsk = LWEKSK::new(&sk_out, &sk_in, 5, 5);
That’s all for the set-up. We now define the vector of messages:
let cipher_max = compute_max_array(&ciphers, &ksk, &bsk, &encoder, &zero)?;
let cipher_min = compute_min_array(&ciphers, &ksk, &bsk, &encoder, &zero)?;
decrypt the result:
let mut max_val = cipher_max.decrypt_decode(&sk_in)?;
let mut min_val = cipher_min.decrypt_decode(&sk_in)?;
round the values:
max_val = (10.*max_val).round() / 10.;
min_val = (10.*min_val).round() / 10.;
print the results and return Ok(()):
println!("maximum: {}", max_val);
println!("minimum: {}", min_val);
Ok(())
Running the program using cargo run --release, you should get:
maximum: 0.6 minimum: 0.1
While finding the minimum and maximum of a dataset can already be useful, in practice this truly shines when used as a building block for other algorithms, e.g., sorting an array. In this section, we now show how to implement a basic sorting algorithm working entirely on encrypted data.
Function to compute the maximum and minimum of two numbers
The functions compute_min and compute_max written above are fairly fast (by FHE standards) as they require only one bootstrap each. However, they have two drawbacks which we want to avoid for a full sort function:
They use the function add_centered_inplace, which is not officially documented.
The encoder correction obtained by adding an encryption of 0 is not always perfect, and may require fine-tuning the offset of the encryption of 0.
Here we show a different version using the programmable bootstrap to reset the encoder. To minimise the number of such bootstrap operations, the same function returns both the minimum and the maximum of two numbers.
// compute the maximum and minimum of two encrypted numbers
//
// Arguments:
//
// cipher_1: the first cipher
// cipher_2: the second cipher
// ksk: the key-changing key needed to revert the key change induced by the bootstrap
// bsk: the boostrapping key
// encoder: the encoder to use in the bootstrap
fn compute_max_min(cipher_1: &LWE, cipher_2: &LWE, ksk: &LWEKSK, bsk: &LWEBSK, encoder: &Encoder)
-> Result<(LWE, LWE), CryptoAPIError>
{
// difference between the two ciphers
let cipher_diff = cipher_2.sub_with_padding(&cipher_1)?;
// programmable bootstrap to check if the difference is positive
let mut cipher_diff_pos = cipher_diff.bootstrap_with_function(bsk,
|x| if x >= 0. { x } else { 0. },
encoder)?;
// change the key back to the original one
cipher_diff_pos = cipher_diff_pos.keyswitch(ksk)?;
// add the result to cipher_1
let mut result_max = cipher_1.add_with_padding(&cipher_diff_pos)?;
// subtract the result from cipher_2
let mut result_min = cipher_2.sub_with_padding(&cipher_diff_pos)?;
// reset the encoder
result_max = result_max.bootstrap_with_function(bsk, |x| x, encoder)?;
result_min = result_min.bootstrap_with_function(bsk, |x| x, encoder)?;
result_max = result_max.keyswitch(ksk)?;
result_min = result_min.keyswitch(ksk)?;
Ok((result_max, result_min))
}
This function will be about three times slower than the previous ones, but it eliminates the drift in the encoder.
Sorting algorithm
Once we can find the minimum of an array of numbers, one can sort it by successively computing the minima of the remaining elements. This requires n(n-1) / 2 comparisons, where n is the array size. There are much faster sorting algorithms: for instance, the merge sort algorithm requires only n ⌈log n⌉ / 2 comparisons in the worst case (where log denotes the logarithm in base 2). However, these algorithms involve conditionals which are not straightforward to evaluate homomorphically (for instance, merge sort requires taking one element from each of two arrays to merge and determine which is the largest, a process which can not be directly implemented without leaking information on the data). For this reason, in this article we will stick to a naive algorithm which, while slower, has the advantage of being easy to implement in FHE.
pub fn sort_array(ciphers: &[LWE], ksk: &LWEKSK, bsk: &LWEBSK, encoder: &Encoder)
-> Result<Vec<LWE>, Box<dyn std::error::Error>>
{
// if ciphers contains less than two elements, just return it
if ciphers.len() < 2 {
return Ok(ciphers.to_vec())
}
// vector containing the result
let mut results = ciphers.to_vec();
for i in 0..(ciphers.len()-1) {
for j in (i+1)..ciphers.len() {
let (c_max, c_min) = compute_max_min(&results[i], &results[j], ksk, bsk, encoder)?;
results[i] = c_min;
results[j] = c_max;
}
}
Ok(results)
}
As described above, this algorithm works iteratively: it first finds the minimum value of the array, then the minimum value of the other elements, and so on. To use it, replace the last line in the main function (Ok(())) with
// sort the array
let ciphers_sorted = sort_array(&ciphers, &ksk, &bsk, &encoder)?;
// decrypt the results
let mut decrypted
= ciphers_sorted.iter().map(|c| { c.decrypt_decode_round(&sk_in) })
.collect::<Result<Vec<f64>, CryptoAPIError>>()?;
// round the results
for i in 0..decrypted.len() {
decrypted[i] = (decrypted[i] / precision).round() * precision;
}
// print the result
println!("{:?}", decrypted);
Ok(())
As described in the introduction, the main problem currently facing FHE is speed: the security it provides comes with a huge runtime penalty of between 1,000× to 1,000,000× depending on the kind of computations being performed. This is way too high for most practical applications, so realising the full potential of FHE will require bringing these numbers down to below 10×.
Fortunately, progress in this domain is coming fast. On the algorithmic and software side, newer schemes like TFHE and efficient implementations like Concrete bring orders-of-magnitude speed-ups over earlier frameworks. Taking a slightly different direction, levelled homomorphic encryption can significantly reduce the runtime for evaluating boolean circuits with a pre-determined, small or medium depth.
On the hardware side, the US Defense Advanced research Project Agency (DARPA) has launched a project to explore hardware acceleration of lattice cryptography in general, and FHE in particular. Promising ideas involve large processor caches and registers to work on large integers, as well as dedicated single instruction multiple data (SIMD) instructions.
At Optalysys, we are following a different yet complementary approach: we are developing a silicon-photonic chip to compute the Fourier transform, the main bottleneck in FHE operations, faster and more efficiently than is possible on electronic hardware. Our system is modular and can integrate with both cutting-edge FHE software and hardware to compound the acceleration that each approach brings. We have previously described our technology in these fourarticles (and take a look at our website for even more documentation). Moreover, we can give an estimate for how quickly our system could tackle the problem at hand.
To this end, we have split the above code into two parts: a client side which encrypts and decrypts data, and a server side performing computations on encrypted data, running on different processes with TCP communication between them. We have also modified the server side to make use of a simulator for our upcoming optical chip. The code is not publicly released yet, but can be made available to participants on our hardware beta program. We have run the same problem (sorting an array of 10 values) on an Intel i7–9700K CPU @ 3.60GHz and on our optical simulator and measured the runtime. To make the comparison valid, we subtracted the runtime for key generation, encryption, decryption, and client-server communication.
When running electronically, and after subtracting some overhead, sorting the array took a bit more than 6s. By comparison, the optical simulator indicated the same operation will run in 0.05s on our silicon-optical chip. Our technology can thus accelerate this sequence of FHE operations by two orders of magnitude. Moreover, this speed-up can be compounded with software improvements and other forms of hardware acceleration, each of which could provide further order-of-magnitude improvements in the coming years.
Based on these results, we strongly believe that FHE will become a commercial reality and revolutionise how the world exchanges data in the next few years — and we are ready to be an integral part of this adventure.
For completeness, we show here the full Cargo.toml, lib.rs and main.rs files for this tutorial. We create the new project using cargo new --lib homomorphic_min_max, compile it with cargo build --release, and run the example using cargo run --release.
Cargo.toml:
[package]
name = "homomorphic_min_max"
version = "0.1.0"
edition = "2021"
[dependencies]
concrete = "0.1.11"
src/lib.rs:
pub use concrete::*;
// compute the maximum of two encrypted numbers
//
// Arguments:
//
// cipher_1: the first cipher
// cipher_2: the second cipher
// ksk: the key-changing key needed to revert the key change induced by the bootstrap
// bsk: the boostrapping key
// encoder: the encoder to use in the bootstrap
// zero: an encryption of 0 with inverted encoder with respect to cipher_1 and cipher_2
fn compute_max(cipher_1: &LWE, cipher_2: &LWE, ksk: &LWEKSK, bsk: &LWEBSK,
encoder: &Encoder, zero: &LWE)
-> Result<LWE, CryptoAPIError>
{
// difference between the two ciphers
let cipher_diff = cipher_2.add_centered(&cipher_1.opposite()?)?;
// programmable bootstrap to check if the difference is positive
let mut cipher_diff_pos = cipher_diff.bootstrap_with_function(bsk,
|x| if x >= 0. { x } else { 0. },
encoder)?;
// change the key back to the original one
cipher_diff_pos = cipher_diff_pos.keyswitch(ksk)?;
// add the result to cipher_1
let mut result = cipher_1.add_centered(&cipher_diff_pos)?;
// subtract 0 to reset the encoder offset
result.add_centered_inplace(zero)?;
Ok(result)
}
// compute the minimum of two encrypted numbers
//
// Arguments:
//
// cipher_1: the first cipher
// cipher_2: the second cipher
// ksk: the key-changing key needed to revert the key change induced by the bootstrap
// bsk: the boostrapping key
// encoder: the encoder to use in the bootstrap
// zero: an encryption of 0
fn compute_min(cipher_1: &LWE, cipher_2: &LWE, ksk: &LWEKSK, bsk: &LWEBSK,
encoder: &Encoder, zero: &LWE)
-> Result<LWE, CryptoAPIError>
{
// difference between the two ciphers
let cipher_diff = cipher_2.add_centered(&cipher_1.opposite()?)?;
// programmable bootstrap to check if the difference is positive
let mut cipher_diff_pos = cipher_diff.bootstrap_with_function(bsk,
|x| if x >= 0. { x } else { 0. },
encoder)?;
// change the key back to the original one
cipher_diff_pos = cipher_diff_pos.keyswitch(ksk)?;
// subtract the result from cipher_2
let mut result = cipher_2.add_centered(&cipher_diff_pos.opposite()?)?;
// add 0 to reset the encoder offset
result.add_centered_inplace(zero)?;
Ok(result)
}
/// compute the maximum of an array of encrypted numbers
///
/// ciphers: an array of ciphertexts
/// ksk: the key-changing key needed to revert the key change induced by the bootstrap
/// bsk: the boostrapping key
/// encoder: the encoder to use in the bootstrap
/// zero: an encryption of 0 with inverted encoder with respect to cipher_1 and cipher_2
pub fn compute_max_array(ciphers: &[LWE], ksk: &LWEKSK, bsk: &LWEBSK, encoder: &Encoder, zero: &LWE)
-> Result<LWE, Box<dyn std::error::Error>>
{
// compute the opposite of 0 to reverse the encoder
let zero = zero.opposite()?;
// convert the array of ciphers into an iterator
let mut ciphers_iter = ciphers.iter();
// set the result to the first cipher, or return an error if the iterator is empty
let mut result = ciphers_iter.next().ok_or("Empty cipher array!".to_string())?.clone();
// loop over the other ciphers
for cipher in ciphers_iter {
// get the maximum of the current result and next cipher
result = compute_max(&result, cipher, ksk, bsk, encoder, &zero)?;
}
Ok(result)
}
/// compute the minimum of an array of encrypted numbers
///
/// ciphers: an array of ciphertexts
/// ksk: the key-changing key needed to revert the key change induced by the bootstrap
/// bsk: the boostrapping key
/// encoder: the encoder to use in the bootstrap
/// zero: an encryption of 0 with inverted encoder with respect to cipher_1 and cipher_2
pub fn compute_min_array(ciphers: &[LWE], ksk: &LWEKSK, bsk: &LWEBSK, encoder: &Encoder, zero: &LWE)
-> Result<LWE, Box<dyn std::error::Error>>
{
// convert the array of ciphers into an iterator
let mut ciphers_iter = ciphers.iter();
// set the result to the first cipher, or return an error if the iterator is empty
let mut result = ciphers_iter.next().ok_or("Empty cipher array!".to_string())?.clone();
// loop over the other ciphers
for cipher in ciphers_iter {
// get the minimum of the current result and next cipher
result = compute_min(&result, cipher, ksk, bsk, encoder, &zero)?;
}
Ok(result)
}
// compute the maximum and minimum of two encrypted numbers
//
// Arguments:
//
// cipher_1: the first cipher
// cipher_2: the second cipher
// ksk: the key-changing key needed to revert the key change induced by the bootstrap
// bsk: the boostrapping key
// encoder: the encoder to use in the bootstrap
fn compute_max_min(cipher_1: &LWE, cipher_2: &LWE, ksk: &LWEKSK, bsk: &LWEBSK, encoder: &Encoder)
-> Result<(LWE, LWE), CryptoAPIError>
{
// difference between the two ciphers
let cipher_diff = cipher_2.sub_with_padding(&cipher_1)?;
// programmable bootstrap to check if the difference is positive
let mut cipher_diff_pos = cipher_diff.bootstrap_with_function(bsk,
|x| if x >= 0. { x } else { 0. },
encoder)?;
// change the key back to the original one
cipher_diff_pos = cipher_diff_pos.keyswitch(ksk)?;
// add the result to cipher_1
let mut result_max = cipher_1.add_with_padding(&cipher_diff_pos)?;
// subtract the result from cipher_2
let mut result_min = cipher_2.sub_with_padding(&cipher_diff_pos)?;
// reset the encoder
result_max = result_max.bootstrap_with_function(bsk, |x| x, encoder)?;
result_min = result_min.bootstrap_with_function(bsk, |x| x, encoder)?;
result_max = result_max.keyswitch(ksk)?;
result_min = result_min.keyswitch(ksk)?;
Ok((result_max, result_min))
}
/// sort an array of ciphertexts
pub fn sort_array(ciphers: &[LWE], ksk: &LWEKSK, bsk: &LWEBSK, encoder: &Encoder)
-> Result<Vec<LWE>, Box<dyn std::error::Error>>
{
// if ciphers contains less than two elements, just return it
if ciphers.len() < 2 {
return Ok(ciphers.to_vec())
}
// vector containing the result
let mut results = ciphers.to_vec();
for i in 0..(ciphers.len()-1) {
for j in (i+1)..ciphers.len() {
let (c_max, c_min) = compute_max_min(&results[i], &results[j], ksk, bsk, encoder)?;
results[i] = c_min;
results[j] = c_max;
}
}
Ok(results)
}
src/main.rs:
use homomorphic_min_max::*;
fn main() -> Result<(), Box<dyn std::error::Error>> {
// encoder
let encoder = Encoder::new(0., 1., 4, 2)?;
// expected precision
let precision = 0.2;
// secret keys
let sk_rlwe = RLWESecretKey::new(&RLWE128_1024_1);
let sk_in = LWESecretKey::new(&LWE128_1024);
let sk_out = sk_rlwe.to_lwe_secret_key();
// encryption of 0
let zero = LWE::encode_encrypt(&sk_in, 0., &encoder)?;
// key switching key
let ksk = LWEKSK::new(&sk_out, &sk_in, 5, 5);
// bootstrapping key
let bsk = LWEBSK::new(&sk_in, &sk_rlwe, 5, 5);
// messages
let messages: Vec<f64> = vec![0.2, 0.4, 0.2, 0.6, 0.2, 0.4];
// encrypt the messages
let ciphers: Vec<LWE>
= messages.iter().map(|m| LWE::encode_encrypt(&sk_in, *m, &encoder))
.collect::<Result<Vec<LWE>, CryptoAPIError>>()?;
// perform the calculation
let cipher_max = compute_max_array(&ciphers, &ksk, &bsk, &encoder, &zero)?;
let cipher_min = compute_min_array(&ciphers, &ksk, &bsk, &encoder, &zero)?;
// decrypt
let mut max_val = cipher_max.decrypt_decode(&sk_in)?;
let mut min_val = cipher_min.decrypt_decode(&sk_in)?;
// round the results
max_val = (max_val / precision).round() * precision;
min_val = (min_val / precision).round() * precision;
// print the result
println!("maximum: {}", max_val);
println!("minimum: {}", min_val);
// sort the array
let ciphers_sorted = sort_array(&ciphers, &ksk, &bsk, &encoder)?;
// decrypt the results
let mut decrypted
= ciphers_sorted.iter().map(|c| { c.decrypt_decode_round(&sk_in) })
.collect::<Result<Vec<f64>, CryptoAPIError>>()?;
// round the results
for i in 0..decrypted.len() {
decrypted[i] = (decrypted[i] / precision).round() * precision;
}
// print the result
println!("{:?}", decrypted);
Ok(())
}
News
© 2024 All rights reserved Optalysys Ltd
Subscribe
Sign up with your email address to receive news and updates from Optalysys.
