Some might think of the waves on the ocean surface, while others might think of their use in the vast network of wireless transmitters and receivers that surrounds most of us in daily life. The ability to work out how waves travel, convey information from one point to another, or dissipate away, is essential to their practical use. However, in most cases, working this out isn’t a trivial task.

A particularly powerful and common tool for studying the evolution of waves is the Fourier transform. In short, it involves decomposing a function (real or complex) into simple waves which can be manipulated individually, a much easier task. The Fourier transform is used throughout the technical world

At Optalysys, we are developing a Fourier optical computing system that combines silicon photonics with free-space optics, allowing us to perform Fourier transforms and convolutions more efficiently, by orders of magnitude, than CPUs and GPUs can. In this article, we report experimental results obtained with our first silicon photonics demonstrator showing that wave propagation can be simulated accurately using an optical device. To the best of our knowledge, this is the first experimental demonstration of a silicon photonic system in simulating wave propagation.

Different kinds of waves

We’ve already mentioned a couple of generic examples of waves, but these hardly start to describe the wide range of phenomena they are involved in.

Formally, a ‘wave’ can be defined as a propagating variation of one or more quantities, often with respect to an equilibrium value. This general definition describes very different phenomena, such as:

• Ocean surface waves, mainly generated by wind or geological events and propagating in the upper layer of the ocean.
• Sound waves, making up everything we can hear (and much more).
• Light, which may be seen as a perturbation of the electro-magnetic field.
• Seismic waves, propagating either on the surface or in the interior of the Earth.
• Gravitational waves: disturbances of space-time itself predicted by Einstein’s General Relativity and first observed in 2015 by the LIGO scientific collaboration. (This observation earned Rainer Weiss, Kip Thorne, and Barry Barish the 2017 Nobel Prize in physics.)
• The wave-function associated with a particle in quantum mechanics, and perturbations of quantized fields in quantum field theories.

This list is, of course, far from exhaustive. While each kind of wave has its own specific properties and quirks, they also share many common features and can be described, at least to some extent, by similar or identical mathematical models. Needless to say, simulating these models has important practical applications. Beyond the theoretical interest of understanding phenomena where waves occur, it allows us, for instance, to quickly estimate when and where a tsunami may strike after the detection of sub-oceanic geological activity. To give another scenario with decidedly lower-stakes, wave analysis may guide the design of concert halls to ensure an optimal acoustic quality from any seat.

Wave propagation and free-space optics

The wave propagation problem consists in finding how waves evolve in time. It is one of the most important questions in the study of waves. For instance, going back to the tsunami example given above, if you detect geological activity below the ocean floor then you want to know how seismic and oceanic waves will propagate away from the epicentre to determine if there is a risk the tsunami may strike inhabited land and, if yes, when, where, and with what amplitude. In very few cases, this problem can be solved with as little as pen and paper by writing down some equations and a few lines of algebra. However, these cases are mostly of academic interest. In practice, most situations are far too complicated for that. Numerical simulations on computers are then the only way to reliably estimate how waves propagate.

These numerical simulations can require a lot of compute power, especially when a high precision is needed or when some uncertainty about the initial conditions or medium in which the waves propagate (for instance, in the seismic wave example, there may be some uncertainty about the precise location of the epicentre) require that many simulations are performed to account for all possibilities. As we will explain below, the Fourier transform is often a major bottleneck in these computations. Fortunately, it is possible to make this operation considerably faster and more efficient. The solution is free-space optics.

A broader look at digital signal processing

The study of wave propagation falls in the wider field of digital signal processing (DSP). This is a huge domain with a broad range of applications in:

• Communication systems, where it is used for modulation and demodulation, channel equalization, and echo or background noise cancellation,
• Consumer electronics (notably in audio and video encoding / decoding and speech synthesis / recognition),
• In the music industry (to generate audio effects, reduce background noise, or in synthetic instruments),
• Medical diagnosis (magnetic-resonance imaging, ultrasonic imaging, computer tomography,…),
• Geophysics (mostly in seismology, studies of the Earth upper layers, and oil exploration),
• Astronomy,
• Aviation (through radar and radio navigation),
• Information security (e.g. for steganography and digital watermarking),

… in fact, just about any application that requires us to work with signals produced by sensors.

While we will focus on wave propagation in this article, the concepts and tools we demonstrate are more widely applicable to DSP. In particular, the Fourier transform is one of the main ingredients of many DSP applications. The results we show for the optical Fourier engine can thus be generalized to numerous applications beyond wave propagation.

A bit of theory on wave propagation

In this article, we consider a relatively simple model of wave propagation, which shows the concepts and techniques as directly as possible. Specifically, we make the following assumptions:

We work in two space dimensions (instead of the usual three). This assumption is mostly made to ease visualisation: it is far easier to see how a wave propagates on a two-dimensional surface than inside a three-dimensional volume.

We assume the medium in which the waves propagate is homogeneous. The techniques shown below can be extended to heterogeneous media, but it can make them more involved.

We neglect interactions between waves. The method we follow can also be extended to include interactions, but, again, at the price of a higher complexity. Moreover, many waves we are used to, like sound waves and light, show very little self-interaction. (A prominent counter-example is surface gravity waves in water, whose self-interactions lead to the common “wave breaking” phenomenon that you can see at any beach.)

Finally, we will make an assumption about the mathematical form of the differential equation describing the wave. In short, it amounts to assuming there is only one ‘type’ of wave. Seismic waves, for instance, come in different types: compressional P-waves, transverse S-waves, Rayleigh waves, Love waves, and Stoneley waves. The general form of the equation we use could describe the propagation of any one of these types of waves, although describing them all together requires a more complicate model.

A simple mathematical model

Mathematically, these waves can be described by a complex field, i.e., a function associating a complex number to each point of space and time. In the following, we call this function 𝜙. Physical quantities, like the pressure for sound waves, can be obtained by taking the real or imaginary parts of this field (or some function of them).

The field 𝜙 obeys a partial differential equation of the form

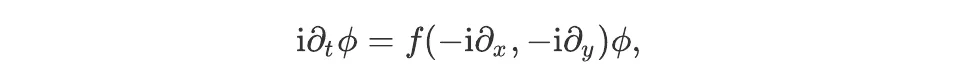
where f is some function, i denotes a complex number such that i² = -1, t is the time coordinate, and x and y are two coordinates in the spatial directions. (There are some technical conditions on the function f for this equation to be well defined.) This equation relates the rate of change of the field 𝜙 describing the wave, on the left of the equal sign, to some function of its space derivatives on the right.

Plane wave solutions

An interesting property of this equation is that it has some (actually, an infinite number of) very simple solutions, of the form

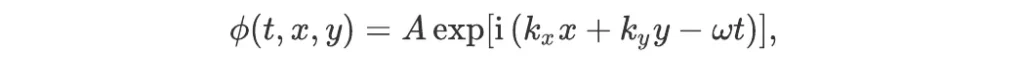
where exp is the exponential function, A is any complex number, and ω, kx, and ky are three numbers such that ω = f(kx,ky). These solutions are called plane waves because their wave-fronts are straight (lines in two dimensions, or planes in three dimensions). The number ω is called the angular frequency of the wave, and the vector k = (kx,ky) its wave vector. This relation between the angular frequency and wave vector is called the dispersion relation. It can be used to infer some important properties of the waves like the speed at which the information and energy it carries propagate.

These solutions are, however, often not very interesting in real-world scenarios. Indeed, they describe waves extending over the whole space with a uniform amplitude. In contrast, most waves of interest are localised; consider the sound emitted from a cello playing one of Bach’s six cello suites, or the burst of light emitted by a distant supernova. In these cases, the amplitude of the waves is highest around the point where they are produced, and drops as the wave expands away. In general, there is no solution with a simple expression that can describe these waves. Fortunately, it is possible to simulate them numerically.

Resolution method

In this section, we sketch how wave propagation can be simulated using the Fourier transform, and how free-space optics can make the calculation faster and more energy-efficient. Our aim here is not to give a mathematically rigorous treatment; instead, we try to keep the presentation relatively simple while giving the key elements needed to understand the resolution method.

Technical assumptions

For the mathematically-oriented readers, let us sketch the assumptions underlying the resolution method we will use. This subsection is a bit more technical than the rest of the article, and can be safely skipped if you are mostly interested in the results — its aim is only to highlight the assumptions under which what we explain below can be made mathematically rigorous.

First, we assume the function 𝜙 is infinitely differentiable in its last two variables, i.e., that its nth derivative with respect to x and mth derivative with respect to y is well-defined for all integer values of n and m. This assumption is slightly stronger than strictly necessary if the function f is a multinomial; but we adopt it to avoid the complications of distinguishing between the cases where f is a multinomial or not.

Second, we assume that 𝜙 and all its derivatives in x and y are square-integrable in these two variables over their domain of definition. For the initial conditions, this means that, for all non-negative integer values of n and m, the integral

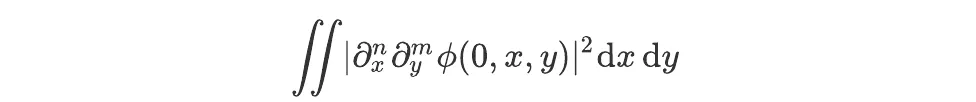
exists and is not infinite. (This assumption could also be slightly relaxed if fis a multinomial.)

Solving the wave equation using the Fourier transform

Let us show how the wave equation can be solved in Fourier space. We denote by F the Fourier transform operator in the space directions (i.e, the last two variables of 𝜙). The wave equation can be rewritten as:

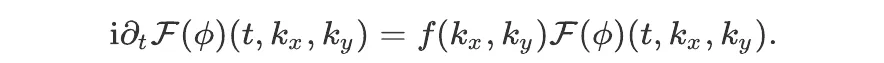
This equation is much simpler than the previous one because the arguments of the function f are now numbers rather than derivatives. Moreover, the remaining derivative is of order one, making the resolution formally easy. The general solution may be written as:

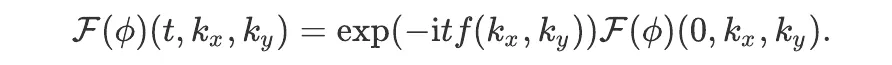
This equation gives the Fourier transform of 𝜙 at time t from its value at some other time (here taken equal to 0). All one has to do to find 𝜙 is then to inverse the Fourier transform.

In summary, starting from some initial condition at t = 0, the value of 𝜙 at an arbitrary time can be obtained in three steps:

• Compute the Fourier transform of the initial condition.
• Multiply by an array of complex exponentials.
• Compute the inverse Fourier transform of the result.

While the wave propagation problem we are considering is a relatively simple one (as it does not include non-linear effects nor heterogeneous media), the same or a similar method is used in algorithms dealing with more involved ones, the main difference being that time must then generally be discretized and the above procedure repeated for each time step.

The optical advantage

Let us briefly comment on the complexity of the above method. There are three operations to consider: the Fourier transform, multiplication by an exponential, and the inverse Fourier transform.

On a CPU or GPU, the most efficient algorithm to perform the Fourier transform is due to James W. Cooley and John W. Tukey and often called the ‘fast Fourier transform’ (see also our previous article). If we work on a discretized grid with N pixels, this algorithm has a complexity in O(N logN). The inverse Fourier transform has the same complexity.

The complex exponential multiplication, on the other hand, has a complexity in O(N). For large grids, it is thus much less demanding than the Fourier transform and its inverse, which are the bottlenecks of the algorithm.

This, at least, is true for electronic hardware. Using free-space optics, the Fourier transform and its inverse can be performed in theoretical O(1)runtime. (See our previous articles for more explanation on how we do it.) Free-space optics can thus completely eliminate the Fourier bottleneck in wave propagation simulation as well as other problems using spectral methods (see another of our articles for an example of an application to the Navier-Stokes equations).