Optalysys - The Optical Fourier Engine

Introduction

The Optical Fourier Engine: A Fourier transform accelerator in arbitrary number of dimensions

Written by Florent Michel

What do post-quantum cryptography, convolutional neural networks, computational fluid dynamics, and signal analysis have in common? They all share an important property: each of them requires a lot of compute power to unleash their full potential and solve practical problems. But there is something else which unites them: they all can make use of the same mathematical operation to become more efficient. This operation is the Fourier transform (FT).

We have already explored some application areas of the FT in lattice-based cryptography, homomorphic encryption, convolutional neural networks with Bayesian uncertainty, transformers, computational fluid dynamics, simulation of wave propagation, self-driving, and neurosymbolic AI. Other application spaces include digital signal processing, time series analysis, image filtering,… In fact, a list of domains where the FT is not useful would likely be shorter than a list of where it is!

As explained in our previous articles, we at Optalysys are currently developing a chip combining silicon photonics and free-space optics to accelerate and reduce the energy cost of 2-dimensional (2D) FTs by several orders of magnitude.

In this article, we will tackle an important question: can we use the optical Fourier engine to do FTs on data that is not 2D? More importantly, what are the implications of using 2D specialised hardware on data that is not 2D? Is there a significant performance penalty if we wish to use our hardware on long 1D sequences rather than large 2D grids?

As we will show here, it is possible to use 2D FTs as a base unit for calculating 1D FTs while keeping most of the optical advantage. From that, it is then possible to build FTs in 3 or more dimensions.

To give a feel for what we will cover, and allow you to pick what you are most interested in, here is an informal, approximate table of contents:

We will first explain in a formal-ish way how the FT performed by the optical device can be used to reconstruct larger 2D ones or 1D ones. We will make some simplifying assumptions to keep the algebra simple, but aim to provide a mostly rigorous explanation.
We will then work through a simple example to show how this idea can be applied in practice.
We will show a Python implementation.
We will explain how to use the previous results to construct higher-dimensional Fourier transforms, with an illustration in 3D.
Finally, we will briefly comment on the performance.

Notations

Let us gather here, for easy reference, the notations that will be used in the rest of the article. This section may be skipped if you are interested in the main idea rather than the mathematical details — but, in case you are interested in these details, here are the keys which will help you understand them.

In this article, arrays (or tensors) are indexed from 1, as is common in linear algebra.
The letter i will denote a square root of -1. In mathematical formulae, we will keep it upright to clearly distinguish it from scalar variables (in italics).
The exponential function will be denoted by exp.
Arrays of numbers will be denoted by boldface Latin letters and their components by the corresponding letters with one or more indices.
We will denote by a curly F with index d the discrete Fourier transform in dimension d. If A is an array (or, to use a slightly more precise word, a real or complex tensor) of shape (N₁, N₂, …), where N₁, N₂, … are positive integers, then the Fourier transform of A is an array (or tensor) with the same shape and coefficients given by

for each value of j₁, j₂, …

Of particular interest will be the Fourier transforms in 1 and 2 dimensions. The formulas are given, respectively, by

and

Let us give two simple examples to make it a bit less formal. In two dimensions, we may for instance consider the case N₁ = N₂ = 2. Then, the input is a square matrix of size two, of the form

The FT of this matrix will also be a square matrix of size 2, given by:

(There is no imaginary part because the exponentials are all integer powers of exp(πi), which is equal to -1. The exponential factors are thus all equal to -1 or 1. This would be different for larger matrices.)

As another example, let us consider a one-dimensional array of the form

Its FT is:

(You may use this formula to check that some of the results we give below are correct.)

The Cooley-Tukey algorithm and generalisation

From 2D to 1D (or larger 2D)

The Cooley-Tukey algorithm is, in short, a way to perform a ‘large’ FT by splitting it into smaller ones which can be done independently. Similar to many other divide and conquer algorithms, its wide adoption is mostly due to its efficiency: while doing an FT of size N using the formulae given above has a complexity O(N²), the Cooley-Tukey algorithm reduces it to O(N log N). For large values of N, i.e., when dealing with large arrays, this is a significant advantage.

Another feature of this algorithm is that each of the smaller transforms requires less resource than the larger one, and can be performed by hardware with a fixed input size. We have already described how it works in a previous article, but let us summarise it succinctly.

To take one example, if N is the number of pixels of the hardware device, an FT of total size N² can be computed in three steps:

First divide the original array of size N² into N arrays of size N and calculate the FT of each individual smaller array.
Multiply each coefficient by a complex number with modulus 1, called a ‘twiddle factor’, and perform some permutation of the entries.
Calculate another FT of each smaller array, and combine the results.

Intuitively, one may say that the first and third steps each executes part of the larger transform, so that doing them sequentially (with multiplication by the twiddle factors and permutation between them) is equivalent to the full operation. When doing a 2D FT, this is exactly what we need. But what if you want a 1D FT instead? Fortunately, this requires only a minor change to this algorithm.

In the above description, the first and last steps are the most computationally intensive: they each require N FTs of size N, with a total complexity in O(N³) when done naively, while the second step has complexity in O(N²). However, it is the second step which determines what they do together. By modifying it just a little, one can change the number of dimensions of the resulting FT from 2 to 1.

In the next subsection, we sketch mathematically why this is true. While we do not aim to be fully rigorous, this subsection will be more technical than the rest of the article, and can be skipped if you are more interested in the results than in exactly why they work.

Mathematical formulation

To keep the notations relatively simple, let us focus on a particular instance of this algorithm. We denote by (nx,ny) the shape of the optical device input array, and assume we want to process an image with shape (nx²,ny²). We will here present two similar algorithms: the Cooley-Tukey algorithm, to compute the 2D FT of the image, and a modified version performing nx² independent 1D FTs (one for each line of the input). We will also make use of several sets of integers. For each positive integer n, we denote by Iₙ the set of all integers between 1 and n (included).

Let us call A the original array. The first step of the Cooley-Tukey algorithm is to separate it into nx ny sub-arrays a⁽ʲ ᵏ⁾ with coefficients given by:

We then take the 2D FTs of each of these sub-arrays, denoting the results with a ‘~’. This defines nx ny arrays, each of them with shape (nx,ny).

The third step is where the standard Cooley-Tukey algorithm and the one yielding the 1D transforms differ. They both involve multiplication by complex numbers with unit modulus, called ‘twiddle factors’, and some data rearrangement. Let us start with Cooley-Tukey. For each (j,k), we define the array b⁽ʲ ᵏ⁾ with shape (nx,ny) by:

The two exponentials in the right-hand side form the twiddle factor (which, in practice, may be pre-computed to reduce the runtime), and the last factor may be seen as the transpose of the tensor made by the coefficients of the previous arrays along two planes.

The algorithm giving one-dimensional FTs works with a slightly simpler twiddle factor, a transposition in one plane only, and a reversal of the coefficients in one direction. For each (j,k), we define the array c⁽ʲ ᵏ⁾ with shape (nx,ny) by:

where we define the modulo operator % in the following way: if n and m are two positive integers, n%m is the integer between 0 and m-1 whose Euclidean division with m has the same remainder as that of n.

The next step, common to the two algorithms, is to compute the 2D FT of each of these arrays. This gives nx ny new arrays with shape (nx,ny) each, denoted with a ‘~’.

Finally, we need to reconstruct the result. Up to a global factor, this step is similar for the two algorithms. Denoting with an index 2 the 2D FT of the array A and by an index 1 the array made of the 1D FTs of its lines, we have, for each (j,k),

where // denotes the Euclidean division, and

Using one of these algorithms, one can thus reconstruct either a larger 2D FT with shape (nx²,ny²) or a batch of nx² 1D transforms with size ny², using 2D FTs with shape (nx,ny) as the main building-blocks.

As a side note, notice that the values of nx and ny used in the first and second FTs do not really need to be equal. Under some conditions, it is thus possible to compute FTs with a different shape than (nx²,ny²). In the remainder of this article, we will mostly stick to this case for simplicity; but keep in mind that it is not a fundamental limitation.

A simple example of batched 1D Fourier transforms from 2D ones

Let us see how the second algorithm works on a practical example. Assume one wants to compute the FTs of the arrays (1,1,1,1), (1,1,1,0), (1,1,0,0), and (1,0,0,0) using a device which can only take arrays with shape (2,2) as inputs. First batch the 4 inputs in a matrix (one per line):

Then separate this matrix into 4 sub-matrices as follows:

The next step is to perform the 2D FT of each sub-matrix:

For larger matrices, one would need to exchange the line j of each sub-matrix with the line nx +1- j for each j between 2 and nx. For nx=2, this is not needed (it would only exchange line 2 with itself, i.e., make no change). The next step is to exchange the columns; in our case, only two of them need to be moved:

One also needs to multiply by the twiddle factors. In the present case, it amounts to multiplying the last column by the complex number -i:

We’re nearly there! There remains to perform again the FT of each sub-matrix…

… divide by nx…

… and do again the permutation of the first step:

The four lines of the resulting matrix, (4,0,0,0), (3,-i,1,i), (2,1-i,0,1+i), and (1,1,1,1) are the FTs of the original ones (1,1,1,1), (1,1,1,0), (1,1,0,0), and (1,0,0,0).

Of course, this example is not very interesting: computing FTs of size 4 is not particularly difficult, and actually simpler than going through this procedure. However, it becomes beneficial when two conditions are satisfied:

the length of the inputs is at least moderately large (say, at least several tens of entries),
you have an efficient way to do the ‘small’ 2D FTs.

Indeed, when using this algorithm to compute N one-dimensional FTs of size N, you need 2N smaller 2D ones and a number O(N²) of other operations. If each of the smaller transforms can be done sufficiently fast (and they will be fast on an optical Fourier engine, which can perform each of them in one single frame), then, the total complexity is in O(N²). By comparison, the complexity of doing the N one-dimensional FTs electronically would be at least in O(N² log N). For large values of N, using a 2D optical device is thus way more efficient.

Python implementation

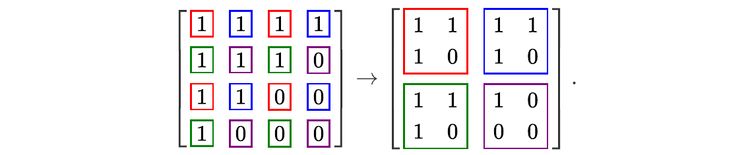
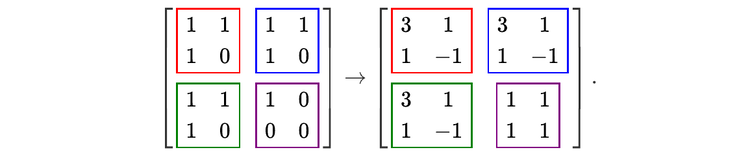
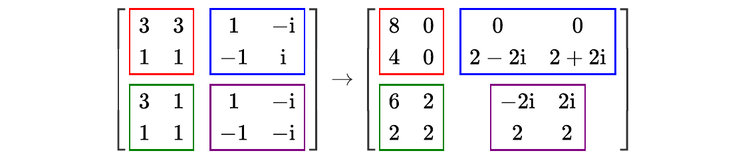
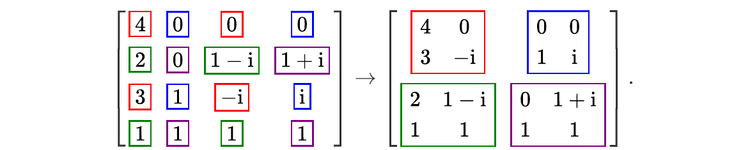
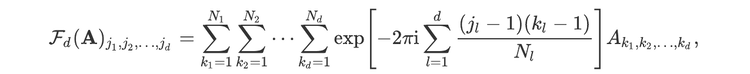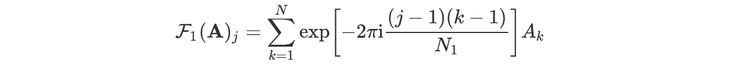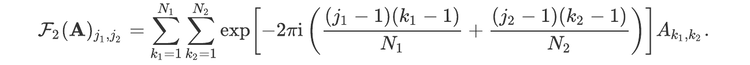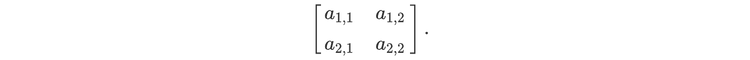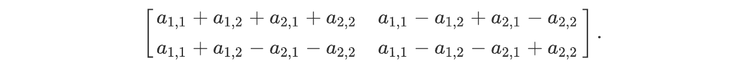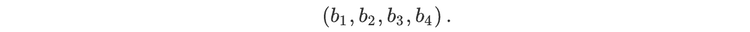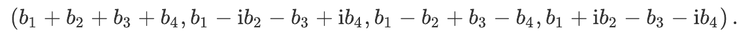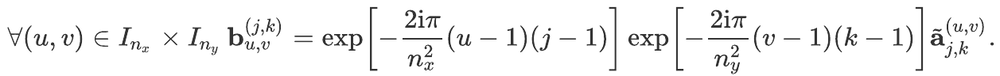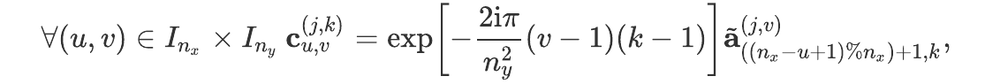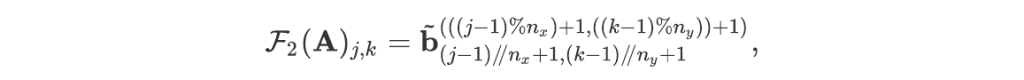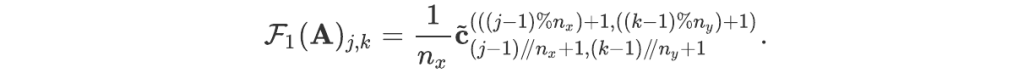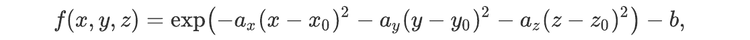For readers who may be more familiar with code than with mathematical notations, here is a Python function implementing this algorithm. It takes as argument a NumPy array, img, with at least two dimensions, and returns the FT along the last dimension. In this script,

nx and ny give the shape of the input for the device (for instance, in the above example, they would both be equal to 2),
device_FT is the 2D Fourier transform done by the optical device (if you want to try this script, you may use np.fft.fft2, as shown in the examples below),
the last two dimensions of the input must have lengths equal to the squares of nx and ny, respectively.

import numpy as np
def FFT1D(img):
    '''
    1D Fourier transforms

    Arguments: 
        img: 2+ dimensional real or complex array of shape (..., nx**2, ny**2)
    '''

    try:
        assert (img.shape[-1]) == nx**2
        assert (img.shape[-2]) == ny**2
    except: 
        print('Wrong image shape: expected ({},{}); got {}'
              .format(nx**2, ny**2, img.shape[-2:]))
        return

    # shape of the batch
    n_imgs = img.shape[:-2]
    d_imgs = tuple(range(len(n_imgs)))

    # create the Fourier transforms of the sub-arrays
    a = img.reshape(n_imgs + (nx,nx,ny,ny)).transpose(d_imgs + (-3,-1,-4,-2))
    tilde_a = device_FT(a)

    # multiply by the complex numbers with modulus 1
    j_jp = np.arange(ny)[:,np.newaxis].dot(np.arange(ny)[np.newaxis,:])
    ey = np.exp(-2.*np.pi*1j/(ny*ny) * j_jp)
    tilde_a_p = tilde_a * ey[np.newaxis,:,np.newaxis,:]
    
    # some rearrangement of the lines
    tilde_a_p[...,1:,:] = tilde_a_p[...,-1:0:-1,:]

    # transpose
    bar_a = tilde_a_p.transpose(d_imgs + (-4,-1,-2,-3))

    # second round of Fourier transforms
    tilde_bar_a = device_FT(bar_a)

    # reconstruct the result
    tilde_A = tilde_bar_a.transpose(d_imgs + (-2,-4,-1,-3))\
                         .reshape(n_imgs + (nx*nx,ny*ny)) / ny

    return tilde_A


Here is an example of use in an IPython instance (after copying the above code in the system clipboard; notice that Python uses the letter j instead of i for the square root of -1):

In [1]: %paste
...
In [2]: device_FT = np.fft.fft2; # use the NumPy fft2 function 
In [3]: nx=2; ny=2; # set nx and ny
In [4]: a = np.array([[1,1,1,1],
   ...:               [1,1,1,0],
   ...:               [1,1,0,0],
   ...:               [1,0,0,0]])
In [5]: print(FFT1D(a).round(15)) 
[[ 4.+0.j  0.+0.j  0.+0.j  0.+0.j]
 [ 3.+0.j -0.-1.j  1.+0.j  0.+1.j]
 [ 2.+0.j  1.-1.j  0.+0.j  1.+1.j]
 [ 1.+0.j  1.+0.j  1.+0.j  1.+0.j]]

Each line of the output is the discrete FT of the corresponding line of the array a. This is, in itself, not very impressive: the function np.fft.fftwould have done exactly the same thing! What is more interesting is that, to perform this calculation, the function FFT1D has only done small 2-dimensional FTs of size 2 by 2—exactly what a (very small) optical device could do!

It is easy to verify that it also works for larger arrays. For instance, changing the values of nx and ny to 3, we can compute the FTs of the arrays (1,1,1,1,1,1,1,1,1), (2,2,2,2,2,2,2,2,2), …, (9,9,9,9,9,9,9,9,9):

In [6]: nx=3; ny=3; # changing the values of nx and ny
In [7]: a = np.ones((9,9)) * np.arange(1,10)[:,np.newaxis]; print(a) # input
[[1., 1., 1., 1., 1., 1., 1., 1., 1.],
 [2., 2., 2., 2., 2., 2., 2., 2., 2.],
 [3., 3., 3., 3., 3., 3., 3., 3., 3.],
 [4., 4., 4., 4., 4., 4., 4., 4., 4.],
 [5., 5., 5., 5., 5., 5., 5., 5., 5.],
 [6., 6., 6., 6., 6., 6., 6., 6., 6.],
 [7., 7., 7., 7., 7., 7., 7., 7., 7.],
 [8., 8., 8., 8., 8., 8., 8., 8., 8.],
 [9., 9., 9., 9., 9., 9., 9., 9., 9.]]
In [8]: print(FFT1D(a))
[[ 9.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j]
 [18.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j]
 [27.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j]
 [36.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j]
 [45.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j]
 [54.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j]
 [63.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j]
 [72.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j]
 [81.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j]]

You can check that the result is correct (the FT of a uniform array has just one non-vanishing coefficient, which is the sum of the input coefficients).

Finally, let us do a check with a 100 by 100 random matrix. It would, of course, be quite cumbersome to check the result by hand. Instead, let us compare the result with that of the function np.fft.fft, which is the NumPy one-dimensional FT implementation, and compute the mean absolute value of the difference:

In [9]: nx=10; ny=10;
In [10]: a = np.random.uniform(size=(100,100))
In [11]: print(np.abs(FFT1D(a) - np.fft.fft(a)).mean())
1.1224604726207545e-15


The difference is not exactly 0; this is because the numbers Python work with do not have an infinite precision. What this result shows is that the two ways of computing the FTs give the same result up to the numerical accuracy of the engine. (You will probably get a slightly different number if you try this code. This is because the matrix a is chosen randomly each time the code is run. But the result should be smaller than 10⁻¹⁴.)

A note on performance

But, if we are using a two-dimensional Fourier engine, are not we wasting resources? Surely a 2D FT of size 100 by 100 is a much more demanding operation than a 1D transform of size 100, so why use an algorithm designed for the former to compute the later? These are entirely valid questions if you want to compute only one such FT: then, doing the equivalent of a large 2D version first is certainly not a good idea. However, the situation changes drastically when you want to do many of them. Just as a GPU is useless for doing a single operation, and really shines when doing multiple calculations in parallel, you can harvest the full potential an optical Fourier engine by doing many FTs.

The reason is that, for instance, a 10 by 10 device can perform 100 different one-dimensional FTs in parallel, for the same runtime as doing a single 2D transform of size 100 by 100. Said otherwise, we use the second dimension to execute many one-dimensional FTs simultaneously. This is why using a two-dimensional optical device can, using this algorithm, be not only competitive with electronic hardware designed for one-dimensional transforms, but significantly more efficient.

From 1D to 3D (and more)

We have shown that a 2D Fourier engine can be used to compute large 2D or 1D FTs. But are we limited to these two dimensions? Fortunately, no: we can combine 2D and 1D transforms to compute higher-dimensional ones. For instance, the 3D FT of a 3D array A with shape (N₁, N₂, N₃) can be computed in two steps:

First, compute the 2D transform along the first two dimensions. This produces N₃ FTs with shape (N₁, N₂).
Then compute the 1D transform of the result along the third dimension. This produces N₁ N₂ FTs with size N₃. Together, they form the 3D Fourier transform of A.

Let us illustrate this on an example. We consider a real-valued function fwith three real arguments, of the form

where ax, ay, and az are three positive constants and x₀, y₀, z₀, and b are four real constants. The first term describes a Gaussian function, whose value decreases, roughly speaking, like the square of the radius from its centre, which is the point with coordinates (x₀, y₀, z₀). The three numbers ax, ay, and az determine how fast it decreases in each direction. So, the iso-surfaces of f (i.e., the surfaces where it has a constant value) are ellipsoids (kinds of deformed spheres, more extended in one or two directions than in the other). The constant b is adjusted so that the mean value of f is 0, to prevent the central value of the FT from becoming too large. The iso-surfaces for this function are shown in the figure below¹:

Example of iso-surfaces for an asymmetric Gaussian function which is more extended in the x direction than in the other two

The figures below are plots of the original function evaluated on a discrete grid with shape (121,121,121), of its 2D transform in the (y,z) plane, and of the 1D transform of the result in x. To make visualisation easier, we shifted the results by half the grid length compared with the definitions used in the previous sections.

Example of decomposition of a 3D Fourier transform as a 2D Fourier transform followed by a 1D one. The left panel shows the input function. The middle panel shows iso-surfaces (after taking the absolute value to get real numbers) of its 2D Fourier transform in the directions y and z. The right panel shows iso-surfaces for (the absolute value of) the 1D Fourier transform of the result in the x direction. One can verify that the result is identical to a 3D Fourier transform of the first Gaussian.

Sums of the three functions shown in the above 3D plots along the x (top line), y (middle line), and z (bottom line) directions. One can notice that the right plot is thinner in the x direction than in the other two, while it was the opposite for the left plot. This is a general property of the Fourier transform: large features tend to be mapped to small ones and conversely.

We could also have shown the 3D FT of f; but, as you may have guessed, it would look exactly like the right plots: by doing a 2D FT followed by a 1D one in the third direction, we have effectively reconstructed the 3D version.

The same technique can be used to reconstruct higher-dimensional FTs. For instance, A 4D transform can be reconstructed as the combination of two 2D ones, a 5D transform as two 2D ones and a 1D one,… More generally, for any positive integer d, one can compute a d-dimensional FT by performing d//2 2D FTs (where // is the Euclidean division) plus a 1D transform if d is odd. In practice, however, the most important cases are d=1 (used, for instance, in signal or time series analysis and in cryptography), d=2 (for classical or deep-learning image processing), and d=3 (for computational fluid dynamics, wave propagation modelling and 3D deep learning CNNs).

Fourier transform at the speed of light

As we mentioned above, the most intensive operations in the Cooley-Tukey algorithm as well as its variation computing batched FTs is the computation of smaller transforms: even if each of them is much easier to do than the large 2D one, they still require, for large arrays, much more compute power than the other steps in these algorithms do. Or, at least, that is true when the algorithm runs on electronic hardware. Free-space optical computing completely changes the picture thanks to a peculiar property of light: the presence of interferences, due to its wave-like nature. We will not go into the details of light propagation here; but, to make a long story short, and under some approximations, a simple parabolic lens is equivalent to the 2D FT, in that the amplitude of the electro-magnetic field (the ‘essence’ of light) in one focal plane is equal to the FT of its amplitude in the other focal plane.

Moreover, the calculation happens literally at the speed of light, as electro-magnetic waves move from one focal plane to the other. Even better, no active component is required in the process, and power dissipation can in principle be reduced to virtually zero. We talked about this optical advantage in our previous articles, to which we refer for more details.

For this reason, an optical Fourier engine can be significantly more efficient than state-of-the-art electronic hardware for the 2D FT, as well as its 1D or higher-dimensional variants using the algorithms described above. Precisely how efficient it is will depend on many factors, like the quality of the optical components, sensitivity of light detectors, and type of interface. The specifications of the device we are developing will be given in a future article, along with quantitative estimates for the gain in efficiency. To give a glimpse of what is to come, let us simply state here that we expect the efficiency boost to be well over an order of magnitude vs the fastest and most efficient modern solutions.

Conclusion

While this article was quite long, the main message is clear and simple: the optical Fourier engine developed by Optalysys will be able to perform any kind of FTs of practical interest. To gather some examples, it can do:

small or large 2D FTs, with countless applications in image analysis and deep learning (a prominent example being convolutional neural networks, possibly including a Bayesian uncertainty estimate, and a more recent one is logic tensor networks; we have also recently proposed that they may be used in transformers),
large 1D FTs, which are at the core of signal analysis algorithms, error-correction codes, and cryptosystems (like the NTRU public-key system, and most other lattice-based systems like those used for post-quantum cryptography or in homomorphic encryption),
large 3D FTs, which can help in computer simulations of fluid dynamicsand wave propagation²,
and higher-dimensional Fourier transforms, if and when the need arises.

Thanks to the peculiar properties of light, the 2D FT can be computed without resorting to any active component and literally at the speed of light, so that optical Fourier engine can be vastly more efficient than state-of-the-art electronic systems.

In light of these arguments, and given the wealth of problems which can be accelerated using this mathematical operation, it seems certain that free-space optical computing will play a major role in the future of computing. The question is not if, but when. And, given the pace of the recent progress, it is increasingly evident that the optical computing revolution is just around the corner.

• • •

¹ The values we used are: ax=0.02, ay=0.01, az=0.02, and x₀=y₀=z₀=60.

² The last two linked articles give examples in 2D to make visualisation easier; but more realistic examples would generally use 3D simulations.